Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 ∘ ; cạnh AB = a. Tính thể tích khối đa diện ABCC'B'
A. 3 4 a 3
B. 3 4 a 3
C. 3 a 3
D. 3 3 4 a 3
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có góc giữa hai mặt phẳng A ' B C và A B C bằng 60 ° , cạnh A B = a . Tính thể tích V của khối lăng trụ A B C . A ' B ' C ' ?
A. V = a 3 3 4 .
B. V = 3 a 3 4 .
C. V = 3 a 3 3 8 .
D. V = a 3 3 .
Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60° AB = a. Khi đó thể tích của khối ABCC'B' bằng:
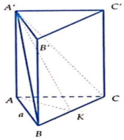
A. a 3 3
B. 3 a 3 4
C. a 3 3 4
D. 3 a 3 3 4
Cho lăng trụ đứng ABC.A'B'C' có cạnh BC=2a, góc giữa hai mặt phẳng (ABC) và (A'BC) bằng 60 ° . Biết diện tích của tam giác ∆ A ' B C bằng 2 a 2 . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = a 3 3
B. V = 2 a 3 3
C. V = a 3 3 3 .
D. V = 3 a 3
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác đều. Điều kiện cần và đủ để góc giữa hai mặt phẳng A ' B C và A B C bằng 60 ° là
A. A ' A A B = 3
B. A ' A A B = 3 2
B. A ' A A B = 3 2
D. A ' A A B = 1 2
Lăng trụ tam giác đều A B C . A ' B ' C ' có góc giữa hai mặt phẳng A ' B C và (ABC) bằng 60 ° ; cạnh A B = a . Thể tích khối đa diện A B C . C ' B ' bằng:
A. 3 a 3 4
B. a 3 3 8
C. 3 a 3 4
D. 3 a 3
Đáp án A
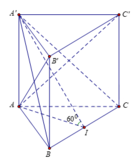
Gọi I là trung điểm của BC. Ta có:
A I = a 3 2 ⇒ A ' A = A I tan 60 ° = 3 a 2
S B C C ' B ' = 3 a 2 a = 3 a 2 2
Thể tích của khối chóp A B C C ' B ' là:
V = 1 3 A I . S B C C ' B ' = 1 3 . a 3 2 . 3 a 2 4 = a 3 3 4
Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 o , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A'B'C' là
A. 2 3
B. - 2
C. 3 3
D. - 3
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, góc giữa mặt phẳng (A'BC ) và mặt phẳng ( ABC ) bằng 45 p . Thể tích của khối lăng trụ ABC.A'B'C' bằng
A. 3 a 3 8
B. a 3 3 2
C. a 3 3 4
D. a 3 3 8
Cho hình lăng trụ tam giác đều
ABC.A'B'C' có cạnh đáy bằng a, góc
giữa mặt phẳng (A'BC ) và mặt phẳng
( ABC ) bằng 45o. Thể tích của khối
lăng trụ ABC.A'B'C' bằng
![]()
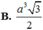
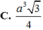
![]()
Cho hình lăng trụ đều A B C . A ' B ' C ' biết góc giữa hai mặt phẳng A ' B C và A B C bằng 45 ° , diện tích tam giác A ' B C bằng a 2 6 . Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ A B C . A ' B ' C ' .
A. 4 π a 2 3 3
B. 2 π a 2
C. 4 π a 2
D. 8 π a 2 3 3
Đáp án C
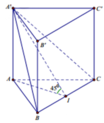
Gọi I là trung điểm của BC. Đặt A ' A = x ⇒ A I = x , A ' I = x 2
Khi đó: B C = 2 B I = 2. A I tan 30 ° = 2 x 3 S A ' B C = 1 2 A I ' . B C = a 2 6 ⇔ 1 2 x 2 . 2 x 3 = a 2 6 ⇔ x = a 3 ⇒ B C = 2 x 3 = 2 a 3 3 = 2 a
Bán kính mặt đáy hình trụ ngoại tiếp hình lăng trụ là R = 2 a 3 4 a 2 3 = 2 a 3
Diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ là S x q = 2 π . 2 a 3 . a 3 = 4 π a 2