(O) và (O') ngoài nhau tiếp chung ngoài AB;CD (A,C e (O); B,D e (O'), tiếp tuyên chung trong MN cắt AB,CD taik E;F ( M e (O) ; N e (O').
a) c/m AB =EF
b) c/m EM = FN
Cho hai đường tròn (O) và (O') ngoài nhau, tiếp tuyến chung trong CD và tiếp tuyến chung ngoài AB ( A , C thuộc (O), B , D thuộc (O')). Chứng minh rằng AC , BD và OO' đồng quy
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (Ạ và C thuộc (O), B và D thuộc (O')). Tiếp tuyến chung trong MN cắt AB và CD theo thứ tự là E và F (M thuộc (O), N thuộc (O')). Chứng minh:
a, AB = EF
b, EM = FN
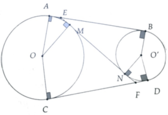
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF
cho đường tròn (O) và (O') ngoài nhau. kẻ tiếp tuyến chung ngoài AB của 2 đường tròn (A thuộc (O), B thuộc (O')). vẽ các tiếp tuyến chung trong của 2 đường tròn lần lượt cắt AB tại C và D. CMR AC = BD
Cho hai đường tròn (O; 6 cm) và (O'; 2 cm) nằm ngoài nhau. Gọi AB là tiếp tuyến chung ngoài, CD là tiếp tuyến chung trong CD của hai đường tròn (A và C thuộc (O); B và D thuộc (O’)). Biết AB = 2CD, tính độ dài đoạn nối tâm OO'
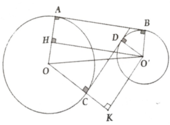
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm
Cho 2 đường tròn O và O' ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB, CD (A,C thuộc đường tròn O; B,D thuộc đường tròn O'). TIếp tuyến chung trong MN cắt AB và CD theo E và F (M thuộc O, N thuộc O')
a. AB=EF
b. EM=FN
Cho 2 đường tròn (O) và(O') ở ngoài nhau. Kẻ tiếp tuyến chung ngoài AB và tiếp tuyến chung trong EF (A,E thuộc(O); B,F thuộc(O'). Gọi M là giao điểm của AB và EF
a) Chứng minh: tam giác AOM đồng dạng tam giác BMO'
b) Chứng minh: AE vuông góc BF
c) Gọi N là giao điểm của AE và BF. Chứng minh: O, N, O' thẳng hàng
Cho hai đường tròn tâm O và O’ tiếp xúc ngoài tại H. Kẻ tiếp tuyến chung ngoài AB, điểm A thuộc tâm O và B thuộc tâm O’ . Tiếp tuyến chung trong tại H cắt tiếp tuyến chung ngoài AB tại M a, Chứng minh rằng góc AHB bằng 90° b, Tính góc OMO’ c, Tính AB biết OH=9cm ,O’H =4cm
Hai đường tròn (O ; R) và (O' ; r) tiếp xúc ngoài với nhau. Gọi AB là tiếp tuyến chung của hai đường tròn, A∈(O),B∈(O′).
a) Tính độ dài AB.
b) Cho R=36cm,r=9cm. Tính bán kính của đường tròn (I) tiếp xúc với đường thẳng AB và tiếp xúc ngoài với hai đường tròn (O) và (O').
Cho (O) bk 9cm và (O') bk 4cm tiếp xúc ngoài tại C. Gọi tiếp tuyến chung ngoài BA với B thuộc (O), A thuộc (O'). Vẽ (I;r) tiếp xúc ngoài với (O) và (O') và tiếp xúc với AB tại N. Tính r