Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2018. Gọi M là trung điểm AA’; N, P lần lượt là các điểm nằm trên các cạnh BB’, CC’ sao cho B N = 2 B ' N , C P = 3 C ' P . Tính thể tích khối đa diện ABCMNP
A. 4036 3
B. 32288 27
C. 40360 27
D. 23207 18
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AA' = a 3 . Gọi I là giao điểm của AB’ và A’B. Cho biết khoảng cách từ I đến mặt phẳng (BCC'B')bằng a 3 2 . Tính thể tích khối lăng trụ ABC.A’B’C’.
A. 3 a 3
B. a 3
a 3 . 3 a 3 4
D. a 3 4
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 72 c m 3 . Gọi M là trung điểm của đoạn thẳng BB’. Tính thể tích khối tứ diện ABCM.
A. 36 c m 3
B. 18 c m 3
C. 24 c m 3
D. 12 c m 3
Chọn D.
Phương pháp:
Lập tỉ số thể tích khối tứ diện ABCM và khối lăng trụ ABC.A’B’C’. Từ đó tính thể tích khối tứ diện ABCM.
Cách giải:
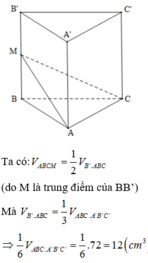
Cho hình lăng trụ đều ABC.A’B’C có AB=2a, AA'=3a Gọi M, N, P lần lượt là trung điểm của AA’, A’C, AC. Tính theo a thể tích V của khối tứ diện B.MNP.
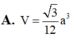
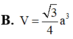
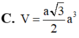
Cho hình lăng trụ đều ABC.A’B’C có A B = 2 a , AA'=3a. Gọi M, N, P lần lượt là trung điểm của AA’, A’C, AC. Tính theo a thể tích V của khối tứ diện B.MNP.
A. V = 3 12 a 3
B. V = 3 4 a 3
C. V = a 3 2 a 3
D. V = 3 8 a 3
Đáp án B.
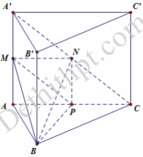
Ta có B P ⊥ A C B P ⊥ A ' A ⇒ B P ⊥ A ' A C ⇒ B P ⊥ M N P
Ta có M N = 1 2 A C = a ; N P = 1 2 A ' A = 3 a 2
⇒ S M N P = 1 2 M N . N P = 3 a 2 4
Ta có B P = 2 a 3 2 = a 3
V B . M N P = 1 3 B P . S M N P = 1 3 . a 3 . 3 a 2 4 = a 3 3 4 .
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 72 cm3. Gọi M là trung điểm của đoạn thẳng BB’. Tính thể tích khối tứ diện ABCM.
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều, M là trung điểm của BC, AA’ = AM = a. Thể tích của lăng trụ bằng:
A. a 2 3 3
B. a 3 3 3
C. a 2 2 2
D. a 3 3 9
Cho hình lăng trụ đứng ABC.A’B’C’ có M là trung điểm của AA’. Tỉ số thể tích V M . A B C V A B C . A ' B ' C ' bằng
A. 1 6
B. 1 3
C. 1 12
D. 1 2
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AA¢ và BB¢. Đường thẳng CM cắt đường thẳng C’A¢ tại P, đường thẳng CN cắt đường thẳng C‘B¢ tại Q. Thể tích của khối đa diện lồi A’MPB’NQ bằng
A. 1
B. 1 3
C. 1 2
D. 2 3
Cho khối lăng trụ ABC. A'B'C' có thể tích bằng 2018. Gọi M là trung điểm AA' ; N, P lần lượt là các điểm nằm trên các cạnh BB', CC' sao cho BN=2B'N, CP=3C'P. Tính thể tích khối đa diện ABC. MNP.
A. 32288 27
B. 40360 27
C. 4036 3
D. 23207 18