Bài 1:
Cho tam giác ABC có BC=4cm. Gọi D,E theo thứ tự là trung điểm của AC,AB; M và N theo thứ tự là trung điểm của BE và CD, MN cắt BD ở P, cắt CE ở Q.
a) Tính độ dài đoạn MN
b) Chứng miinh rằng MP=PQ=QN

Những câu hỏi liên quan
Bài 4: Cho tứ giác ABCD(AB//CD). Gọi E;F;K theo thứ tự là trung điểm của AD;BC;AC.
1) So sánh các độ dài của tam giác MIK
2) Chứng minh EF=AB+CD/2
Bài 5: Cho tam giác ABC có D là trung điểm của AB.Tia Dz//BC cắt AC tại E. chứng minh E là trung điểm của AC
Bài 5:
Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Bài 4:
2: Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF là đường trung bình của hình thang ABCD
=>EF//AB//CD và \(EF=\dfrac{AB+CD}{2}\)
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Biết AH = 8cm, HB = 4cm, HC = 6cm, tính diện tích các tứ giác DECH, BDEF và DEFH.
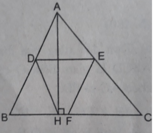
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có độ dài cạnh bằng a. Gọi M là 1 điểm nằm trong tam giác. MI,MP,MQ theo thứ tự là khoảng cách từ M đến các cạnh BC,AB,AC. Gọi O là trung điểm của cạnh BC. Các điểm D và E theo thứ tự chuyển động trên các cạnh AB và AC sao cho widehat{DOE}60^o.
a) Chứng minh: MI+MP+MQ không đổi.
b) Chứng minh: Đường thẳng DE luôn tiếp xúc với một đường tròn cố định.
c) Xác định vị trí của D và E để diện tích tam giác DOE đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo a.
Đọc tiếp
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).
Cho tam giác ABC có BC=4cm. Gọi D,E lần lượt là trung điểm AC, AB; M,N theo thứ tự là trung điểm BE và CD. MN cắt BD ở P, cắt CE ở Q
Cm MP=PQ=QN
cho tam giác ABC : BC = 4cm . Gọi D,E theo thứ tự là trung điểm của AC , AB , M và N theo thứ tự là trung điểm của BE , CD . MN cắt BD ở H , cắt CE ở K
a) tính MN
b) MH= HK = KN
Cho tam giác ABC có BC =4cm , gọi DE theo thứ tự là trung điểm của AC,AB,M,N theo thứ tự là trung điểm của BE và CD , MN cắt BD ở P ,cắt CE ở Q.Chứng minh: a. Tam giác MAD là tam giác cân b. MP=PQ=QP
Bài 8. Cho tam giác ABC, lấy điểm D thuộc cạnh AB, E thuộc cạnh AC sao cho BD=CE. Gọi I, K, M theo thứ tự là trung điểm của BE và CD, BC a) Chứng minh tam giác IMK cân. b) Gọi giao điểm của IK với AB và AC theo thứ tự là G, H. Chứng minh AG=AH. c) Gọi N là trung điểm của DE. Gọi P và Q theo thứ tự là giao điểm của MN với AB và AC. Chứng minh tam giác APQ cân
a: Xét ΔBEC có
I là trung điểm của BE
M là trung điểm của BC
Do đó: IM là đường trung bình của ΔBEC
Suy ra: \(IM=\dfrac{EC}{2}\left(1\right)\)
Xét ΔDCB có
K là trung điểm của DC
M là trung điểm của BC
Do đó: KM là đường trung bình của ΔDCB
Suy ra: \(KM=\dfrac{BD}{2}\)
mà BD=CE
nên \(KM=\dfrac{CE}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra IM=KM
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông ?
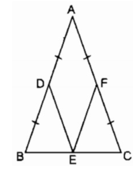
Hình thoi ADEF là hình vuông ⇒ ∠ A = 90 0
⇒ ∆ ABC vuông cân tại A
Ngược lại nếu ∆ ABC vuông cân tại A
⇒ Tứ giác ADEF là hình thoi có ∠ A = 90 0
⇒ Hình thoi ADEF là hình vuông
Vậy hình thoi ADEF là hình vuông thì ∆ ABC vuông cân tại A.
Đúng 0
Bình luận (0)
Cho tam giác ABC, BC = 4cm. Gọi D, E theo thứ tự là trung điểm của AC, AB ; M, N theo thứ tự là trung điểm của BE, CD. MN cắt BD tại P, MN cắt CE tại Q.
a. Tính độ dài đoạn MN
b. Chứng minh rằng MP = PQ = QN
Bạn tự vẽ hình nha
a) Vì D,E là trung điểm của AC và AB nên ED là đường trung bình của tam giác ABC.
Suy ra ED = \(\frac{BC}{2}\)= \(\frac{4}{2}\)= 2 (cm)
Tứ giác EDCB có ED // BC ( Vì ED là đường trung bình của tam giác ABC) nên EDCB là hình thang.
Vì M, N là trung điểm của EB và CD nên MN là đường trung bình của hình thang EDCB
suy ra MN = \(\frac{ED+BC}{2}\)= \(\frac{2+4}{2}\)=3 (cm).
Vậy MN =3 (cm)
b) Ta có MN// ED ( MN là đương tb củahình thang EDCB) nên MP//ED , QN//ED
Xét tg EBD có MP//ED (cmt)
MB =ME (gt)
Suy ra P là trung điểm của BD ,nên MP là đương tb của tg EBD nên MP= \(\frac{ED}{2}\)=\(\frac{2}{2}\)= 1(cm).
Chứng minh tương tự với tg ECD cũng có QN = 1(cm)
Ta có MN = MP + PQ +QN
3 = 1+PQ +1
QN =1 (cm)
Nên MP=PQ=QN.(đpcm)
Có nhìu chỗ thiếu xót mong mấy bạn thông cảm.
Đúng 0
Bình luận (0)
Nếu c/m tứ giác MEDN là hình thang thì s bn ơi..................?????
Đúng 0
Bình luận (0)














