Đường tròn nội tiếp (I) của tam giác ABC lần lượt tiếp xúc với BC,CA, AB tại D,E,F; ID cắt EF tại N, AI cắt BC tại K. CMR:
a) \(\frac{EN}{EI}=\frac{AK}{AC}\)
b) AN đi qua trung điểm của BC
Những câu hỏi liên quan
Cho tam giác ABC , AB> AC ngoại tiếp đường tròn (I ) và nội tiếp đường tròn (O). Đường tròn (I ) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi H là hình chiếu vuông góc của D trên EF. Đường tròn ngoại tiếp tam giác AEF cắt đường tròn (O) tại K (K khác A).
a) Chứng minh HD là phân giác của góc BHC .
b) Chứng minh ba điểm I, H, K thẳng hàng.
Cho tam giác ABC có đường tròn nội tiếp (I) tiếp xúc với ba cạnh BC, CA, AB lần lượt tại D, E, F. BI cắt EF tại K. Chứng minh rằnga)△BFK∽△BIC; b) BKC = 90
a) Ta dễ chứng minh \(\widehat{BIC}=90^o+\dfrac{\widehat{A}}{2}\).
Ta thấy \(\widehat{BFK}=\widehat{A}+\widehat{AEF}=\dfrac{\widehat{A}}{2}+\widehat{IAE}+\widehat{AEF}\) \(=90^o+\dfrac{\widehat{A}}{2}\)
Nên \(\widehat{BIC}=\widehat{BFK}\)
Xét 2 tam giác BIC và BFK, ta có:
\(\widehat{FBK}=\widehat{IBC}\) (do BI là tia phân giác của \(\widehat{FBC}\)) và \(\widehat{BIC}=\widehat{BFK}\left(cmt\right)\)
\(\Rightarrow\Delta BIC~\Delta BFK\left(g.g\right)\) (đpcm)
b) Từ \(\Delta BIC~\Delta BFK\Rightarrow\dfrac{BI}{BF}=\dfrac{BC}{BK}\) \(\Rightarrow\dfrac{BI}{BC}=\dfrac{BF}{BK}\)
Xét 2 tam giác BIF và BCK, ta có
\(\dfrac{BI}{BC}=\dfrac{BF}{BK}\) và \(\widehat{IBF}=\widehat{CBK}\)
\(\Rightarrow\Delta BIF~\Delta BCK\left(c.g.c\right)\)
\(\Rightarrow\widehat{BKC}=\widehat{BFI}\)
Mà \(\widehat{BFI}=90^o\) nên \(\widehat{BKC}=90^o\) (đpcm)
Đúng 3
Bình luận (0)
Cho đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với 3 cạnh BC,CA,AB tại D,E,F. Qua E vẽ đường thẳng song song với BC cắt AD,DF lần lượt tại M,N. CM M là Trung điểm của EN
Cho tam giác ABC có cạnh BC nhỏ nhất, đường tròn (I) nội tiếp tam giác và tiếp xúc ba cạnh BC,CA,AB lần lượt tại D,E,F. Gọi M,N lần lượt là hai điểm đối xứng của C,B qua E,F. Các đường thảng BM,CN cắt EF lần lượt tại K,L. Chứng minh rằng DK// và D thuộc trung trực của Kl
Cho hình vẽ:Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Đọc tiếp
Cho hình vẽ:
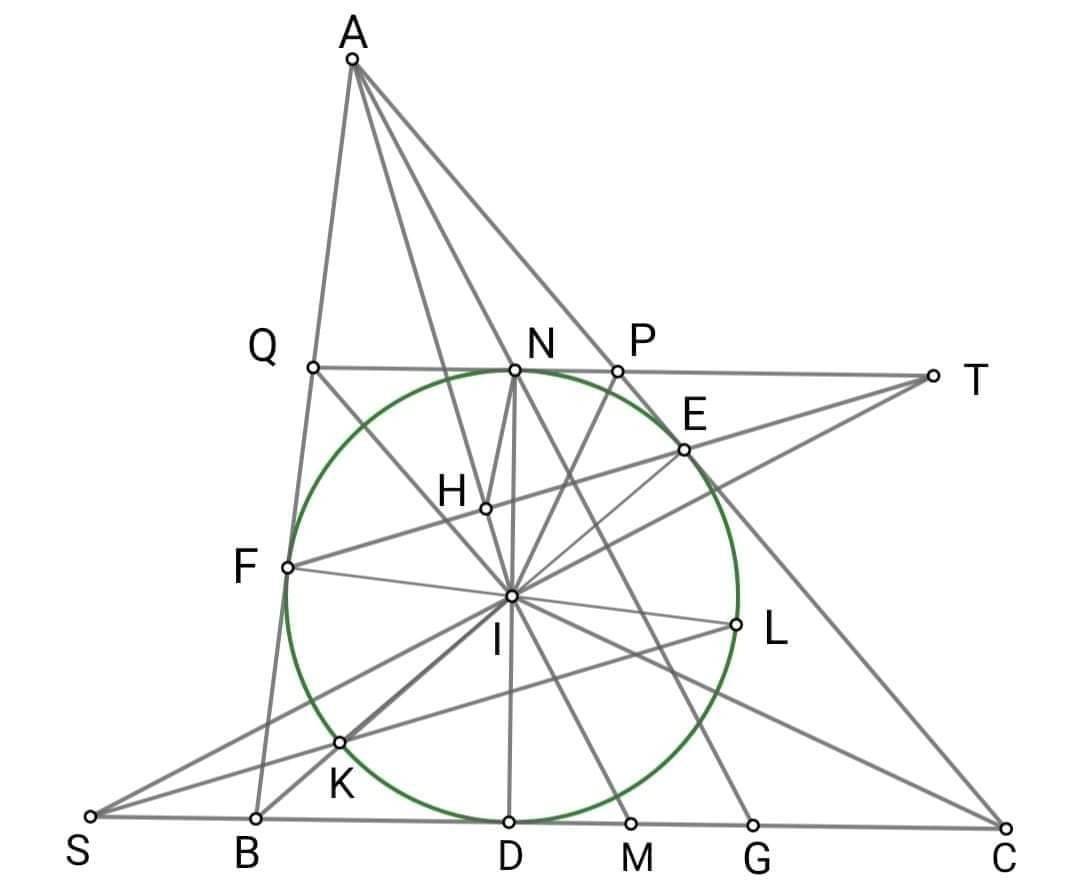Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD = r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Cho tam giác ABC đường tròn nội tiếp tam giác tiếp xúc với các cạnh BC,CA , AB lần lượt tại các điểm M,N,P . các đoạn thẳng nối tâm đường tròn với các đỉnh cắt đường tròn lần lượt tại D,E,F.gọi I là iao điểm của MD và NE .CMR IP I
Cho tam giác ABC, đường tròn tâm I nội tiếp tam giác tiếp xúc với các cạnh AB, AC, BC lần lượt tại D, E và F. DE cắt BC tại P. IF cắt đường tròn đường kính BC tại K.
CMR : PK là tiếp tuyến của đường tròn đường kính BC
15 tháng 11 2023 lúc 21:40
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). Đường tròn (J) bàng tiếp góc A tiếp xúc với các đường thẳng BC, CA, AB lần lượt tại D, E, F. Gọi M là trung điểm của BC. Đường tròn đường kính MJ cắt DE tại điểm K khác D. Gọi D là giao điểm thứ hai của đường thẳng AD và (J) .
a) Chứng minh rằng bốn điểm B, D, K, D cùng nằm trên một đường tròn.
b) Gọi G là giao của BC và EF, đường thẳng GJ cắt AB, AC lần lượt tại L và N. Lấy các điểm P, Q lần lượt trên các đường thẳng JB, JC sao cho...
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). Đường tròn (J) bàng tiếp góc A tiếp xúc với các đường thẳng BC, CA, AB lần lượt tại D, E, F. Gọi M là trung điểm của BC. Đường tròn đường kính MJ cắt DE tại điểm K khác D. Gọi D là giao điểm thứ hai của đường thẳng AD và (J) .
a) Chứng minh rằng bốn điểm B, D, K, D' cùng nằm trên một đường tròn.
b) Gọi G là giao của BC và EF, đường thẳng GJ cắt AB, AC lần lượt tại L và N. Lấy các điểm P, Q lần lượt trên các đường thẳng JB, JC sao cho \(\widehat{PAB}=\widehat{QAC}=90^o\). Các đường thẳng LP và NQ cắt nhau tại T. Gọi S là điểm chính giữa cung BAC của (O) và T là giao của AT với (O). Chứng minh rằng đường thẳng ST' đi qua tâm đường tròn nội tiếp tam giác ABC.
Cho tam giác ABC nhọn (AB>AC) ngoại tiếp đường tròn tâm I. Đường tròn (I) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Đường thẳng EF cắt (I) tại N (khác D). Cm MN là tiếp tuyến của đường tròn (I).
Cho tam giác ABC nhọn (AB>AC) ngoại tiếp đường tròn tâm I. Đường tròn (I) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Đường thẳng EF cắt (I) tại N (khác D). Cm MN là tiếp tuyến của đường tròn (I).