Cho y= x - 2m -1 ( m là hàm số, tính theo toạ độ giao điểm A; B voi trục Ox ,Oy
H là hình chiếu của O trên AB
Xác định m đe OH = √ 2/2
Cho hàm số y=(1-2m)x+3 a) tìm m biết đồ thị hàm số đi qua điểm A(1;0) b) tìm m biết đồ thị hàm số đi qua điểm B(2;-4) c) tìm toạ độ giao điểm của 2 đồ thị hàm số ở câu a,b
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
Cho hàm số y = -1/3x và hàm số y = x-4
a, vẽ đồ thị hàm số y = -1/3x
b,chứng tỏ M (3;-1) là giao điểm của hai đồ thị hàm số trên
c , Tính độ dài OM ( O là góc toạ độ)
Cho hàm số y = 2x có đồ thị là (D1) và hàm số y = 2 /1 x – 3 có đồ thị là (D2). a) Vẽ (D1), (D2) trên cùng một mặt phẳng toạ độ. b) Tìm toạ độ giao điểm của (D1) và (D2) bằng phép tính
Bạn ghi rõ đề ở chỗ (d2) là pt nào đi bạn
Cho 2 hàm số y = f(x) = 2x + 5 và y = g(x) = x + 3. Tính toạ độ M là giao điểm của 2 đồ thị (không vẽ đồ thị)
Cho hàm số y=4-2x (d1) và y=3x+1 (d2) a) Vẽ (d1) và (d2) trên cùng mặt phẳng toạ độ b) Gọi A là giao điểm của (d1) và (d2). Tìm toạ độ giao điểm A c) Tính góc tạo bởi (d1) với trục hoành Tính góc tạo bởi (d2) với trục hoành
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}4-2x=3x+1\\y=3x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{9}{5}+1=\dfrac{14}{5}\end{matrix}\right.\)
Cho parabol(P):y= x^2 và đường thẳng(d):y=x+2
a)Vẽ đồ thị 2 hàm số trên,trên cùng 1 hệ trục toạ độ
b) Xác định toạ độ giao điểm A,B của 2 đồ thị trên
c) Cho điểm M thuộc Parabol(P) có hoành độ là m nhỏ thoả mãn
-1 ≤m ≤2. Chứng minh Diện tích MAB ≤ 27/8
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow x^2-2x+x-2=0\)
\(\Leftrightarrow x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Vậy: A(2;4) và B(-1;1)
Cho 2 hàm số y= 2x-3 (d1) và y= \(\dfrac{1}{2}\)x+3 (d2)
a, Vẽ đths y= 2x-3 trên hệ toạ trục Oxy
b, Gọi giao điểm của 2 đường thẳng (d1) và (d2) là M. Tìm toạ độ điểm M bằng phương pháp đại số
GIÚP MÌNH VỚI
a: 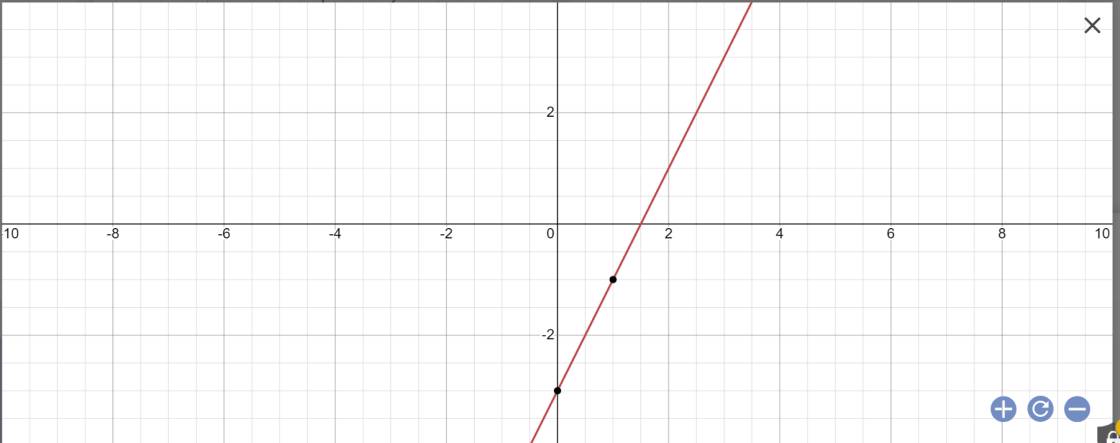
b: Phương trình hoành độ giao điểm là:
\(2x-3=\dfrac{1}{2}x+3\)
=>\(2x-\dfrac{1}{2}x=3+3=6\)
=>\(\dfrac{3}{2}x=6\)
=>\(x=6:\dfrac{3}{2}=4\)
Thay x=4 vào y=2x-3, ta được:
\(y=2\cdot4-3=5\)
Vậy: M(4;5)
Cho hàm số \(y=(2m-1)x+m-1\) . Xác định m để:
a) Hàm số nghịch biến trong R
b)Đồ thị hàm số cắt trục hoành tại điểm có hoành độ -1
c) Đồ thị hàm số đi qua điểm M(1;4) . Khi đó vẽ đồ thị hàm số. Tính khoảng cách từ gốc toạ độ O đến đường thẳng đó
a) Hàm số nghịch biến trên R <=> a < 0
<=> 2m - 1 < 0
<=> 2m < 1
<=> m < 1/2
b) Gọi điểm bị cắt là A ( x;y )
cắt trục hoành tại điểm có tọa độ -1
=> x = -1 ; y = 0
=> A ( -1 ; 0 )
Ta có y = ( 2m - 1)x + m - 1 cắt A ( -1;0 )
=> 0 = ( 2m -1 ). ( -1 ) + m - 1
<=> -2m + 1 + m - 1 =0
<=> -m = 0
<=> m = 0
Vậy khi m = 0 thì đồ thị của hàm số cắt trục hoành tại điểm có hoành độ -1
c)
Vì đồ thị của hàm số ( đtchs ) đi qua M(1;4) nên thay điểm M vào đtchs ta được:
4 = ( 2m - 1).1+m - 1
<=> 4 = 2m - 1 + m - 1
<=> 4 = 3m - 2
<=> 6 = 3m
<=> m = 2 ( 1 )
Gọi \(E\left(x_E;y_E\right)\)là điểm nằm trên trục tung vào được đtchs đi qua
Và ta có \(x_E=0\) ( vì xE trùng với góc tọa độ ) ( 2 )
Thay ( 1 ) và ( 2 ) vào đtchs ta được:
y = ( 2 . 2 - 1 ). 0 + 2 - 1
y = 2 - 1
y = 1
Áp dụng hệ thức lượng vào tam giác OEF vuông tại O
\(\frac{1}{OH^2}=\frac{1}{OE^2}+\frac{1}{OF^2}\)
\(\Leftrightarrow\frac{1}{OH^2}=\frac{1}{1^2}+\frac{1}{\left(-1\right)^2}\)
\(\Leftrightarrow\frac{1}{OH^2}=2\)
\(\Leftrightarrow2OH^2=1\)
\(\Leftrightarrow OH^2=\frac{1}{2}\)
\(\Leftrightarrow\orbr{\begin{cases}OH=\frac{\sqrt{2}}{2}\left(nhận\right)\\OH=-\frac{\sqrt{2}}{2}\left(loại\right)\end{cases}}\) ( loại -v2/2 vì độ dài không có giá trị âm )
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng đó là \(\frac{\sqrt{2}}{2}\)
HỌC TỐT !!!!
Gọi (d1) là đồ thị hàm số y = m x + 2 và
(d2) là đô thị hàm số y = 1 x – 1 2
a) Với m = - 12 , xác định toạ độ giao điểm của (d1) và (d2)
b) Xác định giá trị của m để M(- 3; - 3) là giao điểm của (d1) , (d2)