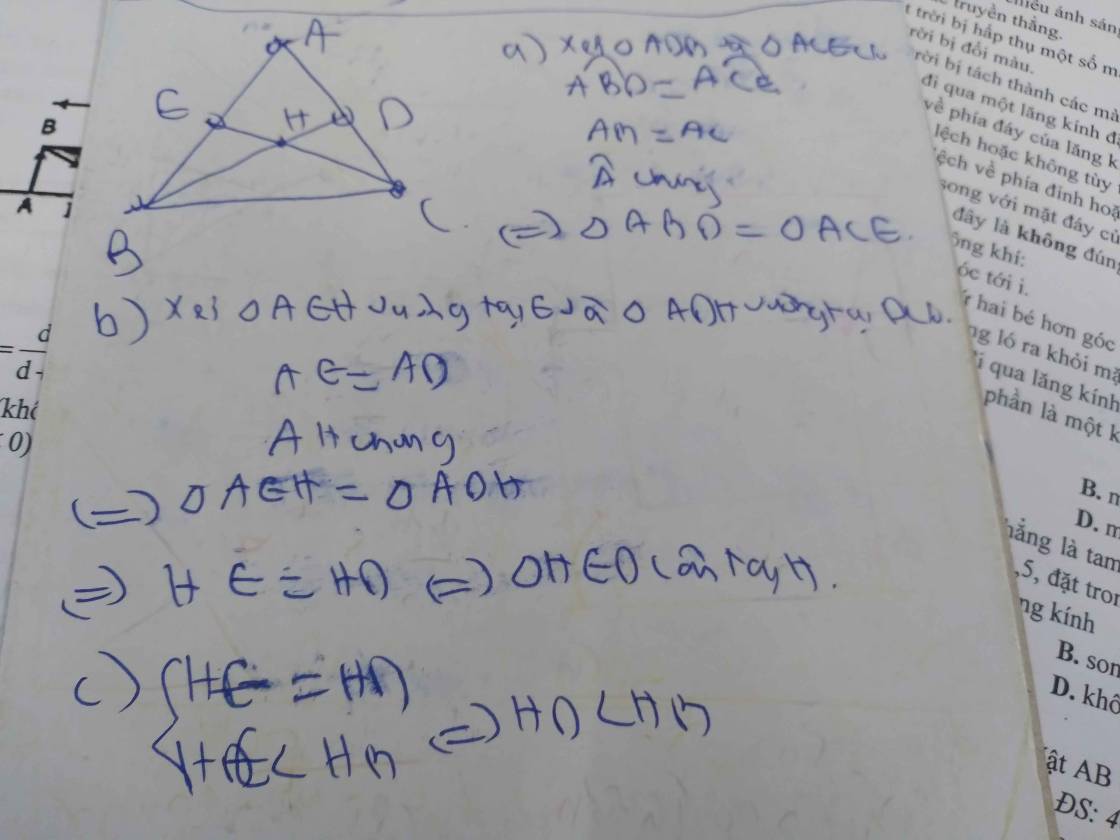
Cho tam giác ABC cân tại C có AB=\(\sqrt{3}\)đường cao CH=\(\sqrt{2}\).Gọi Mlà trung điểm cưa HB , N là trung điểm cưa BC ; AN và CM cắt nhau tại K chứng minh AK/CM=2

Những câu hỏi liên quan
Cho tam giác ABC cân tại C, cạnh AB=\(\sqrt{3}\) , đường cao CH\(=\sqrt{2}\) .Gọi M là trung tuyế của HB, N là trung điểm của BC. AN và CM cắt tại K. CMR: KA=2KM
mình cũng hk pt làm mak thầy cho,neu pn co cau tra loi nho cho minh pt nha
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại C, AB=\(\sqrt{3}\) đường cao CH=\(\sqrt{2}\), M là trung điểm của HB, N là trung điểm của BC, AN và CM cắt nhau tại K. chứng minh KA=2KM
giúp mình với các bạn thân iu ơi. mình cảm ơn nhiều
Cho tam giác ABC cân tại A có đường cao AH. Biết AB= 10cm,BH= 6cm. a) tính độ dài cạnh AH, AC, CH b) chứng minh HB=HC c) gọi M là trung điểm của AC; N là trung điểm của AD. Chứng minh NM//BC
a, Xét tam giác HBA vuông tại H có:
AB2=AH2+BH2(định lí py ta go)
hay 100=AH2+36
=> AH2=64
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
d) Vì AB = AC; BD = CE
mà AB - BD = AD
AC - CE = AE
=> AD = AE
Vì ΔHDE cân
=> H ∈ đường trung trực cạnh DE (1)
Xét ΔADHvàΔAEHcó
AD = AE (cmt)
AH (chung)
DH = HE (cmt)
Do đó: ΔADH=ΔAEH(c−c−c)
=> AD = AE ( hai cạnh tương ứng)
=> ΔADE cân tại A
=> A ∈ đường trung trực cạnh DE (2)
(1); (2) => A,H ∈ đường trung trực cạnh DE
=>AH là đường trung trực cạnh DE
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
các bạn ơi giúp mình với
1, cho tam giác ABC cân tại C , AB=\(\sqrt{3}\), đường cao CH =\(\sqrt{2}\). M là trung điểm của HB, N là trung điểm của BC , AN và CM cắt nhau tại K. Chứng minhKA=2KM
giúp mình với các bạn nhé. mong các bạn trả lời nhiệt tình và nhanh hết sức có thể vì mình đang cần gấp. Cảm ơn các bạn nhiều!
Cho tam giác cân ABC tại C. AB=căn3 ,Đường cao CH=căn2. M là trung điểm của HB,N là trung điểm của BC,AN cắt CM tại K
CMR: AK=2KM
cho tam giác ABC có AB <AC đường cao AH. gọi 3 điểm D,E,F lần lượt là trung điểm của AB,AC,BC
a, tứ giác BDEF là hình gì?
b, cm tứ giác DEFK là hình thang cân
c, gọi H là trực tâm của tam giác ABC; M,N,P theo thứ tự là trung điểm của HA,HB,HC. CM các đường thẳng MF ,NE ,PD bằng nhau và cắt nhau tại trung điểm của mỗi đường
cho tam giác ABC có AB<AC đường cao AH .gọi 3 điểm D,E,F lần lượt là trung điểm của AB,AC,BC
a, tứ giác BDEF là hình gì?
b, CM tứ giác DEFK là hình thang cân
c, Gọi H là trực tâm của tam giác ABC. M,N,P theo thứ tự là trung điểm của HA,HB,HC .CM các đoạn thẳng MF,NE,PD bằng nhau và cắt nhau tại trung điểm của mỗi đường
Cho tam giác ABC cân tại A có đường cao BD và CE cắt nhau tại H.a,chứng minh tam giác ADB=tam giác AEC,b,Chứng minh tam giác HDE là tam giác cân,c,So sánh HB và HD,d,Gọi M là trung điểm của HC,N là trung điểm của HB,I là giao điểm của BM và CN.Chứng minh ba điểu A,H,I thẳng hàng
help với:(((
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 1
Bình luận (0)