a) Để chứng minh tứ giác ABFM là tứ giác nội tiếp, ta cần chứng minh góc AMB + góc AFB = 180 độ.

Góc AMB là góc giữa đường chéo BD và cạnh AB của hình vuông ABCD. Vì đường chéo BD cắt AE tại M, nên góc AMB chính là góc EAM.

Góc AFB là góc giữa đường thẳng EF và cạnh AB của hình vuông ABCD. Vì đường thẳng EF song song với cạnh AB, nên góc AFB bằng góc EAF.

Theo đề bài, góc EAF + 45 độ = 180 độ. Do đó, góc EAF = 180 - 45 = 135 độ.

Vậy, ta có góc AMB + góc AFB = góc EAM + góc EAF = 135 độ + 135 độ = 270 độ = 180 độ.

Vì tổng hai góc AMB và AFB bằng 180 độ, nên tứ giác ABFM là tứ giác nội tiếp.

b) Khi E và F di động trên các cạnh BC và CD của hình vuông ABCD, ta cần chứng minh rằng đường thẳng EF luôn tiếp xúc với một đường tròn cố định.

Gọi O là giao điểm của đường chéo BD và đường thẳng EF. Ta cần chứng minh rằng O nằm trên một đường tròn cố định khi E và F di động.

Vì góc EAF + 45 độ = 180 độ, nên góc EAF = 135 độ. Điều này có nghĩa là tam giác EAF là tam giác cân tại A.

Do đó, đường trung tuyến MN của tam giác EAF là đường cao và đường trung trực của cạnh EF. Vì M và N lần lượt là giao điểm của đường trung tuyến MN với AE và AF, nên M và N là trung điểm của AE và AF.

Vì M và N là trung điểm của hai cạnh của hình vuông ABCD, nên OM và ON là đường trung trực của AB và AD. Do đó, O nằm trên đường trung trực của cạnh AB và AD.

Vì AB và AD là hai cạnh cố định của hình vuông ABCD, nên đường trung trực của AB và AD là đường thẳng cố định. Vậy, O nằm trên một đường tròn cố định.

Vì vậy, khi E và F di động trên các cạnh BC và CD của hình vuông ABCD, đường thẳng EF luôn tiếp xúc với một đường tròn cố định.

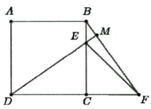
Chứng minh được:

C B F ^ + B E M ^   =   M D F ^ + D E C ^ = 90 0

=>  B M D ^ = 90 0  nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜  của đường tròn đường kính BD

em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.

Helpppppppppppppppppppp

Xét hai tam giác vuông AKD và EAB có:

AD=AB

KD=EB

Do đó :tam giác AKD=TAM GIÁC EAB(2 cạnh góc vuông)

góc KAD= góc EAB

Mà góc DAF+EAB=45ĐỘ

SUY RA:KAF=45 ĐỘ

TAM GIÁC KAF= TAM GIÁC EAF(CGC)

SUY RA KF=FE ;GỌI a LÀ ĐỘ DÀI CẠNH HÌNH VUÔNG ABCD

CHU VI TAM GIÁC EFC LÀ:

EF+FC+CE

=KF+FC+EC

=KD+EC+DF+FC

=BE+EC+DE+EC=a+a=2a

a/

Ta có

\(\widehat{BAE}+\widehat{DAE}=\widehat{ABC}=90^o\)

\(\widehat{FAD}+\widehat{DAE}=\widehat{FAE}=90^o\)

\(\Rightarrow\widehat{BAE}=\widehat{FAD}\)(1)

Ta có \(AB=AD\) (2)

Xét tg vuông BAE và tg vuông DAF

Từ (1) và (2) \(\Rightarrow\Delta BAE=\Delta DAF\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)

\(\Rightarrow AE=AF\Rightarrow\Delta AEF\)  cân tại A

Mà \(\widehat{FAE}=90^o\Rightarrow\Delta AEF\) vuông cân tại A

Xét \(\Delta AEF\) có

IE=IF

\(\Rightarrow AD\perp EF\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao)

Xét \(\Delta KEF\) có

IE=IF; \(AD\perp EF\)

\(\Rightarrow\Delta KEF\) là tg cân (trong tg đường cao xp từ đỉnh đồng thời là đường trung tuyến thì tg đó là tg cân) \(\Rightarrow KE=KF\)

b/

Ta có \(\Delta AEF\) vuông cân tại A \(\Rightarrow\widehat{AFE}=\widehat{AEF}=45^o\) (1)

Xét \(\Delta ABD\) có

AB=AD; \(\widehat{BAD}=90^o\Rightarrow\Delta ABD\) vuông cân tại A \(\Rightarrow\widehat{ADB}=\widehat{ABD}=45^o\) (2)

Từ (1) và (2) \(\Rightarrow\widehat{ADB}=\widehat{AEF}\) (3)

Gọi P là giao của AD với EF; Q là giao của BD với AE

Xét \(\Delta AFP\) và \(\Delta ABQ\) có

AD=AB

\(\Delta AEF\) cân tại A => AF=AE

\(\widehat{DAF}=\widehat{BAE}\left(cmt\right)\)

\(\Rightarrow\Delta AFP=\Delta ABQ\left(c.g.c\right)\Rightarrow\widehat{APF}=\widehat{AQB}\)

Mà \(\widehat{APF}=\widehat{DPI};\widehat{AQB}=\widehat{EQI}\) (góc đối đỉnh)

\(\Rightarrow\widehat{DPI}=\widehat{EQI}\) (4)

Nối D với I, B với I. Xét \(\Delta DPI\) và \(\Delta EQI\)

Từ (3) và (4) \(\Rightarrow\widehat{DIP}=\widehat{EIQ}\)

Mà \(\widehat{EIQ}+\widehat{FIB}=\widehat{FIE}=180^o\)

\(\Rightarrow\widehat{DIP}+\widehat{FIB}=\widehat{DIB}=180^o\) => D; I; B thẳng hàng

c/ 

Ta có \(AM=AB-BM;CE=BC-BE\)

Mà \(BM=BE;AB=BC\)

\(\Rightarrow AM=CE\)

Ta có AD=CD

\(S_{\Delta ADM}=\frac{AD.AM}{2}=S_{\Delta CDE}=\frac{CD.CE}{2}\Rightarrow S_{\Delta ADM}+S_{\Delta CDE}=2S_{\Delta CDE}=CD.CE\)

\(S_{\Delta BME}=\frac{BE.BM}{2}=\frac{BE^2}{2}\)

Gọi a là cạnh hình vuông ABCD có

\(S_{\Delta DEM}=S_{ABCD}-\left(S_{\Delta ADM}+S_{\Delta CDE}+S_{BME}\right)=\)

\(=a^2-2S_{\Delta CDE}-\frac{BE^2}{2}=a^2-a.CE-\frac{\left(a-CE\right)^2}{2}=\)

\(=\frac{2a^2-2a.CE-a^2+2a.CE-CE^2}{2}=\frac{a^2-CE^2}{2}\)

\(\Rightarrow S_{\Delta DEM}\) lớn nhất khi \(a^2-CE^2\) lớn nhất \(\Rightarrow CE^2\) nhỏ nhất => CE nhỏ nhất

CE nhỏ nhất khi CE=0 => E trùng C

a: Xét ΔAFD vuông tại D và ΔAEB vuông tại B có

AD=AB

góc FAD=góc EAB

Do đó: ΔAFD=ΔAEB

b: ΔAFD=ΔAEB

=>AF=AE

=>ΔAFE cân tại A

mà AI là trung tuyến

nên AI vuông góc với EF

Xét ΔINE vuông tại I và ΔIMF vuông tại I có

IE=IF
góc IEN=góc IFM

Do đó: ΔINE=ΔIMF

=>IN=IM

Xét tứ giác MFNE có

I là trung điểm chung của MN và FE

MN vuông góc với FE

Do đó: MFNE là hình thoi