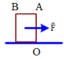
Cho một thanh gỗ hình hộp chữ nhật như hình vẽ có khối lượng 50kg với OA = 80cm; AB = 40cm. Xác định lực F → tối thiểu đế làm quay khúc gỗ quanh cạnh đi qua O. Lấy g = 10 m / s 2
A. 100N
B. 50N
C. 250N
D. 150N
Cho một thanh gỗ hình hộp chữ nhật như hình vẽ có khối lượng 50 kg với OA=80cm;AB=40cm. Xác định lực F → tối thiểu để làm quay khúc gỗ quanh cạnh đi qua O. Lấy g=10m/s2
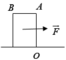
Ta có
P = m g = 50.10 = 500 ( N )
Theo điều kiện cân bằng của Momen lực
M F → = M P → ⇒ F . d F = P . d P V ớ i d P = A B 2 = 40 2 = 20 ( c m ) d F = A O 2 = 80 2 = 40 ( c m ) ⇒ F .0 , 4 = 500.0 , 2 ⇒ F = 250 ( N )
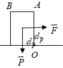
Cho một thanh gỗ hình hộp chữ nhật như hình vẽ có khối lượng 50 kg với AD = 80cm; AB = 40cm. Xác định lực
F
→
tối thiểu để làm quay khúc gỗ quanh cạnh đi qua D. Lấy g=10m/s2
A. 300N
B. 250N
C. 400N
D. 550N
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ).
Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng:

A. 8 c m 3
B. 24 c m 3
C. 12 c m 3
D. 36 c m 3
Chọn A.
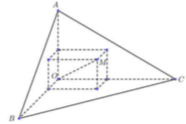
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó ![]()
Hay ![]()
![]()
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có 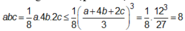 (Theo bất đẳng thức Cô-sin).
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 8( c m 3 ) khi a = 4b = 2c
![]()
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt phẳng (ABC) người ta đánh dấu một điểm M, sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ).
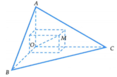
Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng
A. 8 cm3.
B. 24 cm3.
C. 12 cm3.
D. 36 cm3.
Chọn đáp án A
Gọi a, b, c lần lượt là khoảng cách từ điểm M đến các mặt phẳng (OAB),(OBC) và (OCA) (a,b,c > 0).
Ta có V O . A B C = V M . O A B + V M . O B C + V M . O C A
![]()
![]()
Thể tích của khối gỗ là
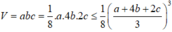
= 1 8 . 12 3 3 = 8 c m 3
Dấu “=” xảy ra khi và chỉ khi khi a =4b =2c =4
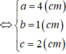
Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện .Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng:
A. 8 c m 3 .
B. 24 c m 3 .
C. 12 c m 3 .
D. 36 c m 3 .
Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó
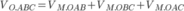
Hay 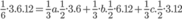

Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có :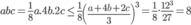 (Theo bất đẳng thức Cô-sin).
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 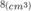 khi
khi
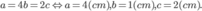
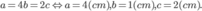
Lan ghép một khối gỗ hình lập phương với một khối gỗ hình hộp chữ nhật có kích thước như hình vẽ bên rồi sơn màu lên các mặt của của hình mới.Tính tổng diện tích Lan phải sơn
cao hoàng nhật minh,à trong sách bạn nha
một khối gỗ hình hộp chữ nhật có kích thước các cạnh AB=40cm, BC=80cm, vật có trọng lượng là P được đặt trên mặt phẳng nằm ngang.
a) Tác dụng vào điểm A một lực theo phương AB. Tính lực tối thiểu để có thể làm nhất khối gỗ lên( khối gỗ quay quanh điểm C)
b)Tác dụng vào A một lực theo phương như thế nào để có thể làm quay khối gỗ quanh điểm C với lực tác dụng nhỏ nhất và lực tác dụng lớn nhất. Tính các lực đó
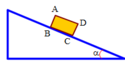
Khối gỗ hình hộp hình chữ nhật có tiết diện thẳng là hình chữ nhật ABCD với AB = 20 cm, AD = 10 cm đặt trên mặt phẳng nghiêng góc α như hình vẽ. Giả thiết ma sát đủ lớn để không xảy ra sự trượt. Tìm α lớn nhất để khối hộp không bị lật.
A. 63 , 4 °
B. 30 °
C. 60 °
D. 26 , 6 °
Một khối gỗ hình hộp chữ nhật có các kích thước như hình bên, người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 4cm. Tính thể tích phần gỗ còn lại.
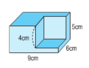
Thể tích khối gỗ lúc đầu là:
9 x 6 x 5 = 270 (cm3)
Thể tích phần cắt đi là:
4 x 4 x 4= 64 (cm3)
Thể tích phần gỗ còn lại là:
270 – 64 = 206 (cm3)
Đáp số: 206cm3