Gọi S là tập nghiệm của phương trình log5(x+1) + log5( x-3) 1. Tìm S A.S {-2; 4} B. 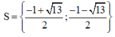C. S {4} D.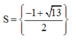
Đọc tiếp
Gọi S là tập nghiệm của phương trình log5(x+1) + log5( x-3) = 1. Tìm S
A.S= {-2; 4}
B. 
C. S= {4}
D. 
Những câu hỏi liên quan
Gọi S là tập nghiệm của phương trình
log
5
(
x
+
1
)
+
log
5
(
x
-
3
)
1
Tìm S A.
S
-
2
;
4
B.
S
-
1
+...
Đọc tiếp
Gọi S là tập nghiệm của phương trình log 5 ( x + 1 ) + log 5 ( x - 3 ) = 1 Tìm S
A. S = - 2 ; 4
B. S = - 1 + 13 2 ; - 1 - 13 2
C. S = 4
D. S = - 1 + 13 2
Giải bất phương trình
log
5
-
1
4
x
-
3
log
5
-
1
2
x
-
1...
Đọc tiếp
Giải bất phương trình log 5 - 1 4 x - 3 > log 5 - 1 2 x - 1 Chọn tập nghiệm S của bất phương trình.
A. 3 4 , 1
B. 1 , + ∞
C. 1 2 , 1
D. 3 4 , + ∞
Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log5( x2 + 1) log5( x2 + 4x + m) - 1 (1) A. -12 ≤ m ≤ 13 B. 12 m 13 C. -12 m 12 D. Đáp án khác
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log5( x2 + 1) > log5( x2 + 4x + m) - 1 (1)
A. -12 ≤ m ≤ 13
B. 12 < m < 13
C. -12 < m < 12
D. Đáp án khác
Tìm tất cả các giá trị thực của tham số m để bất phương trình
1
+
log
5
(
x
2
+
1
)
≥
log
5
(
m
x
2
+
4
x
+
m
)
có nghiệm đúng
∀
x
A.
m
∈
(
2
;
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log 5 ( x 2 + 1 ) ≥ log 5 ( m x 2 + 4 x + m ) có nghiệm đúng ∀ x
A. m ∈ ( 2 ; 3 ]
B. m ∈ ( - 2 ; 3 ]
C. m ∈ [ 2 ; 3 )
D. m ∈ [ - 2 ; 3 )
Tìm tất cả các giá trị thực của tham số m để bất phương trình
1
+
log
5
(
x
2
+
1
)
≥
log
5
(
m
x
2
+
4
x
+
m
)
có nghiệm đúng
∀
x
A.
m
∈
(...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log 5 ( x 2 + 1 ) ≥ log 5 ( m x 2 + 4 x + m ) có nghiệm đúng ∀ x
A. m ∈ ( 2 ; 3 ]
B. m ∈ ( - 2 ; 3 ]
C. m ∈ [ 2 ; 3 )
D. m ∈ [ - 2 ; 3 )
Phương trình log 5 x + 5 = 2 có nghiệm là
A. x = 20
B. x = 5
C. x = 27
D. x = 30
Tổng tất cả các nghiệm của phương trình l o g 5 ( 6 - 5 x ) = 1 - x bằng
A. 2
B. 1
C. 0
D. 6
Biết bất phương trình
l
o
g
5
(
5
x
-
1
)
.
l
o
g
25
(
5
x
+
1
-
5
)
≤
1
có tập nghiệm là đoạn [a;b]. Giá trị của a+b bằng A.
2
+
log
5...
Đọc tiếp
Biết bất phương trình l o g 5 ( 5 x - 1 ) . l o g 25 ( 5 x + 1 - 5 ) ≤ 1 có tập nghiệm là đoạn [a;b]. Giá trị của a+b bằng
A. 2 + log 5 156
B. - 1 + log 5 156
C. - 2 + log 5 156
D. - 2 + log 5 26
Chọn đáp án C
Phương pháp
Giải bất phương trình bằng cách đưa về bất phương trình bậc hai, ẩn là
Đúng 0
Bình luận (0)
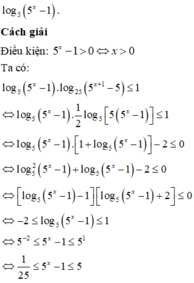
Giải bất phương trình log 5 ( 2 x + 7 ) < 1 + log 5 ( x - 4 )
A. x>4
B. 4<x<9
C. x>9
D. 6<x<10
