Ba mặt phẳng x + 2y - z = 0; 2x - y + 3z + 13 = 0; 3x - 2y + 3z + 16 = 0 cắt nhau tại điểm A. Tọa độ của A là:
A. A(-1;2;-3).
B. A(1;-2;3).
C. A(-1;-2;3).
D. A(1;2;3).
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng (P): x-2y+z-1=0;(Q): x-2y+z+8=0;(C): x-2y+z=0 Một đường thẳng d thay đổi cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của T = A B 2 + 144 A C
A. 72 3 3
B. 96.
C. 108.
D. 72 4 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba mặt phẳng P : x - 2 y + z - 1 = 0 , Q : x - 2 y + z + 8 = 0 và R : x - 2 y + z - 4 = 0 . Một đường thẳng d thay đổi cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của biểu thức T = A B 2 + 144 A C
A. 72 3 3
B. 96.
C. 108.
D. 72 4 3
Chọn đáp án C
Dễ thấy mặt phẳng (P) nằm giữa hai mặt phẳng (Q) và (R) ; ba mặt phẳng (P), (Q), (R) đôi một song song với nhau.
Trên mặt phẳng (P) lầy điểm M(1; 0; 0)
Gọi B’, C’, lần lượt là hình chiếu của A trên hai mặt phẳng (Q) và (R). Ta có :
![]()
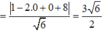
![]()
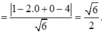
![]()
![]()
![]()
![]()
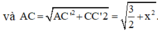
Khi đó
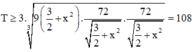
Dấu ‘=’ xảy ra khi và chỉ khi
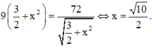
Ba mặt phẳng x+2y-z-6=0 , 2x-y+3z+13=0, 3x-2y+3z+16=0 cắt nhau tại điểm A. Tọa độ của A là:
A. (-1;2;-3)
B. (1;-2;3)
C. (1;2;3)
D. (-1;-2;3)
Cho mặt phẳng P : x - 2 y + z + 5 = 0 , Viết phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
A. (α): 11x-2y-15z+3=0
B. (α): 11x+2y-15z-3=0
C. (α): 11x-2y+15z-3=0
D. (α): 11x-2y-15z-3=0
Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d
Cho mặt phẳng (P): x-2y+z+5=0. Viết phương trình mặt phẳng α vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
![]()
![]()
![]()
![]()
Ba mặt phẳng x + 2 y - z - = 0 , 2 x - y + 3 a + 13 = 0 , 3 x - 2 y + 3 z + 16 = 0 cắt nhau tại điểm A. Tọa độ của A là:
A. A(-1;2;-3)
B. A(1;-2;3)
C. A(-1;-2;3)
D. A(1;2;3)
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng ( P ) : x + 2 y + z - 4 = 0 Có tất cả bao nhiêu mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với ba trục toạ độ x ' O x , y ' O y , z ' O z
A. 8 mặt cầu.
B. 4 mặt cầu.
C. 3 mặt cầu.
D. 1 mặt cầu.
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P):x+2y+z-4=0. Có tất cả bao nhiêu mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với ba trục toạ độ x'Ox, y'Oy, z'Oz?
A. 8 mặt cầu.
B. 4 mặt cầu.
C. 3 mặt cầu.
D. 1 mặt cầu.
Trong không gian với hệ toạ độ Oxyz, cho ba mặt phẳng ( α ) : x + 2 y - z - 1 = 0 , ( β ) : 2 x + y - z - 3 = 0 cùng đi qua một đường thẳng. Giá trị của biểu thức a + b bằng
A. 3.
B. 0.
C. - 3
D. 6.