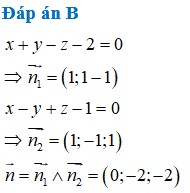Viết phương trình mặt phẳng: Đi qua A(0; -1; 2) và song song với giá của mỗi vec tơ u → = (3; 2; 1) và v → = (-3; 0; 1).
Những câu hỏi liên quan
Viết phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng x+y-z-2=0, x-y+z-1=0
A. x+y+z-3=0
B. y+z-2=0
C. x+z-2=0
D. x-2y+z=0
Viết phương trình mặt phẳng: Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Cách 1:
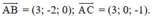
Mặt phẳng (R) đi qua ba điểm A, B, C nhận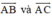 
là hai vec tơ chỉ phương
⇒ Nhận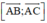 
= ((-2).(-1) – 0; 0.3 – 3.(-1); 3.0 – 3.(-2)) = (2; 3; 6) là vec tơ pháp tuyến.
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Cách 2 :
(R) đi qua A(-3 ; 0 ; 0) ; B(0 ; -2 ; 0) ; C(0 ; 0 ; -1) nên có phương trình đoạn chắn là :
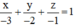
⇔ 2x + 3y + 6z + 6 = 0.
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng (Q) đi qua hai điểm O(0;0;0), A(3;0;1) và vuông góc với mặt phẳng
(
P
)
:
x
+
2
y
-
2
z
+
5
0
A. 2x-7y-6z0 B. 3x+4y-6z0 C. 2x-7y+6z+10 D. x+y+z-40
Đọc tiếp
Viết phương trình mặt phẳng (Q) đi qua hai điểm O(0;0;0), A(3;0;1) và vuông góc với mặt phẳng ( P ) : x + 2 y - 2 z + 5 = 0
A. 2x-7y-6z=0
B. 3x+4y-6z=0
C. 2x-7y+6z+1=0
D. x+y+z-4=0
Chọn A
Mặt phẳng (Q) qua điểm O và nhận vectơ pháp tuyến là tích có hướng của vecto OA và vecto pháp tuyến của mặt phẳng (P)
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng (Q) đi qua hai điểm O(0;0;0), A(3;0;1) và vuông góc với mặt phẳng (P): x+2y-2z+50
Đọc tiếp
Viết phương trình mặt phẳng (Q) đi qua hai điểm O(0;0;0), A(3;0;1) và vuông góc với mặt phẳng (P): x+2y-2z+5=0
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0. A. (P) : 2y + 2z - 1 0 B. (P) : y + z - 1 0 C. (P) : y - z + 3 0 D. (P) : 2x + z - 2 0
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0
B. (P) : y + z - 1 = 0
C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0.
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1). A.
2
x
+
3
y
+
6
z
+
6
0
B.
2
x
-
3
y
+
6
z
+
6
0
C.
x
3
+...
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1).
A. 2 x + 3 y + 6 z + 6 = 0
B. 2 x - 3 y + 6 z + 6 = 0
C. x 3 + y 2 + z 1 = 1
D. x 3 + y 2 + z 1 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng
α
:
x
−
4
y
+
z
0
. Viết phương trình mặt phẳng
β
đi qua A và song song với mặt phẳng
α
. A.
x
−
4
y
+
z
−
4
0
B.
x
−
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng α : x − 4 y + z = 0 . Viết phương trình mặt phẳng β đi qua A và song song với mặt phẳng α .
A. x − 4 y + z − 4 = 0
B. x − 4 y + z + 4 = 0
C. 2 x + y + 2 z − 10 = 0
D. 2 x + y + 2 z + 10 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
−
1
;
2
;
3
và hai mặt phẳng
P
:
x
−
2
0
và
Q
:
y
−
z
−
1
0
. Viết phương trình mặt phẳng đi qua A và vuông góc với hai mặt phẳng ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A − 1 ; 2 ; 3 và hai mặt phẳng P : x − 2 = 0 và Q : y − z − 1 = 0 . Viết phương trình mặt phẳng đi qua A và vuông góc với hai mặt phẳng P , Q
A. x + y + z − 5 = 0
B. x + z = 0
C. y + z − 5 = 0
D. x + y + 5 = 0
Đáp án C
Ta có n P → 1 ; 0 ; 0 ; n Q → 0 ; 1 ; − 1 suy ra n → = n P → ; n Q → = 0 ; 1 ; 1
Suy ra phương trình mặt phẳng cần tìm là: y + z − 5 = 0
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
2
;
3
và mặt phẳng
α
:
x
−
4
y
+
z
0
. Viết phương trình mặt phẳng
β
đi qua A và song song với mặt phẳng
α
. A.
x
−
4
y
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và mặt phẳng α : x − 4 y + z = 0 . Viết phương trình mặt phẳng β đi qua A và song song với mặt phẳng α .
A. x − 4 y + z − 4 = 0
B. x − 4 y + z + 4 = 0
C. 2 x + y + 2 z − 10 = 0
D. 2 x + y + 2 z + 10 = 0
Đáp án B.
Vì β song song với α nên loại đáp án C và D.
Thử trực tiếp thấy điểm A 1 ; 2 ; 3 thuộc mặt phẳng x − 4 y + z + 4 = 0 .
Do đó đáp án đúng là B.
Đúng 0
Bình luận (0)