Tìm tập nghiệm S của bất phương trình ln x 2 < 0
A. S = (-1; 1)
B. S = (0; 1)
C. (-1; 0)
D. ( - 1 ; 1 ) \ { 0 }
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Tìm tập nghiệm của bất phương trình ( 2 x - 7 ) ln ( x + 1 ) > 0
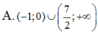
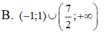
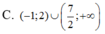
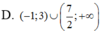
Tìm tập nghiệm S của bất phương trình 2 2 x + 1 - 3 . 2 x - 2 < 0
A. S=R
B. S=(-1,1)
C. S= - ∞ , 0
D. - ∞ , 1
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F ( 0 ) = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + l n ( e x + 1 ) = 3
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Tìm tập nghiệm của bất phương trình ln x 2 < 0
A. S = (-1;1)
B. S = (0;1)
C. S = (-1;0)
D. S = (-1;1)\{0}
Điều kiện: ![]()
Bất phương trình ![]()
Đối chiếu điều kiện ta được tập nghiệm S = (-1;1)\{0}
Chọn D.
Tập nghiệm của bất phương trình - 3 x 2 + x + 4 ≥ 0 là:
A. S = ∅
B. S = (-∞; -1] ∪ [4/3; +∞]
C. S = [-1; 4/3]
D. S = (-∞; +∞)
Tìm tập nghiệm S của bất phương trình 5 x + 1 - 1 5 > 0
A. S = - ∞ ; - 2
B. S = 1 ; + ∞
C. S = - 2 ; + ∞
D. S = - 1 ; + ∞
Tìm tập nghiệm S của bất phương trình 3 x + 1 − 1 3 > 0.
A. − 1 ; + ∞ .
B. − ∞ ; − 2 .
C. − 2 ; + ∞ .
D. − ∞ ; − 1 .