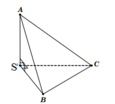
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc với nhau và S A = 2 3 ; S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC.
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Cho hình chóp S.ABC có SA;SB;SC đôi một vuông góc với nhau và S A = 2 3 , S B = 2 , S C = 3. Tính thể tích khối chóp S.ABC
A. V = 12 3
B. V = 4 3
C. V = 2 3
D. V = 6 3
Đáp án C
Thể tích khối chóp là V = 1 6 .2 3 .2.3 = 2 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và S A = 2 3 , SB=2; SC=3. Tính thể tích khối chóp S.ABC
A. V = 6 3
B. V = 4 3
C. V = 2 3
D. V = 12 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA= 2 3 , SB=2, SC=3Tính thể tích khối chóp S.ABC
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.
A. a 3 2
B. a 3 6
C. a 3 24
D. a 3 12
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a. Tính thể tích của khối chóp S.ABC.
A. 1 3 a 3
B. 1 2 a 3
C. 1 6 a 3
D. 2 3 a 3
Đáp án C
Thể tích của khối chóp S.ABC có SA, SB, SC đôi một vuông góc nhau là: V = 1 6 S A . S B . S C = a 3 6
Cho hình chóp S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC 5, thể tích khối chóp S.ABC bằng
A. 20.
B. 30.
C. 10.
D. 60.
Phương pháp:
Thể tích tứ diện vuông là V = 1 6 abc
Cách giải:
Thể tích ![]()
Chọn C.
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng:
A. 300
B. 900
C. 600
D. 450
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 5 a 6
B. 6 a 7
C. 7 a 6
D. 6 a 5
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.
A. V = 1 6 a b c
B. V = 1 3 a b c
C. V = a b c
D. V = 1 2 a b c
Đáp án A
Phương pháp:
Thể tích khối chóp vuông
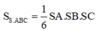
Cách giải:
S.ABC có SA, SB, SC đôi một vuông góc với nhau
⇒ S.ABC là tứ diện vuông tại đỉnh S
