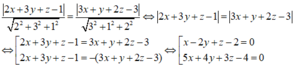Phương trình mặt phẳng cách đều hai mặt phẳng
là (P): x + 2y + 2z - 3 = 0; (Q): x + 2y + 2z = 7 là
![]()
![]()
![]()
![]()
Phương trình mặt phẳng cách đều hai mặt phẳng (P): x+2y+2z-3=0, (Q): x+2y+2z=7 là:
A. (R): x+2y+2z+4=0
B. (R): x+2y+2z-4=0
C. (R): x+2y+2z-5=0
D. (R): x+2y+2z+5=0
Trong không gian Oxyz cho hai mặt phẳng (P) và (P’) lần lượt có phương trình x + 2y - 2z +1 =0 và x – 2y + 2z -1 =0 Gọi (S) là tập hợp các điểm cách đều hai mặt phẳng (P) và (P’). Mệnh đề nào dưới đây đúng ?
A. (S) là mặt phẳng có phương trình x = 0
B. (S) là mặt phẳng có phương trình 2y – 2z + 1=0
C. (S) là đường thẳng xác định bởi giao tuyến của hai mặt phẳng có phương trình x = 0 và 2y – 2z + 1=0
D. (S) là hai mặt phẳng có phương trình x = 0 và 2y – 2z + 1=0
Cho mặt phẳng P : x - 2 y + z + 5 = 0 , Viết phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
A. (α): 11x-2y-15z+3=0
B. (α): 11x+2y-15z-3=0
C. (α): 11x-2y+15z-3=0
D. (α): 11x-2y-15z-3=0
Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d
Cho mặt phẳng (P): x-2y+z+5=0. Viết phương trình mặt phẳng α vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng ( P ) : x + 2 y + 2 z - 10 = 0 . Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 7 3 là
A. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z - 17 = 0
B. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z + 17 = 0
C. x + 2 y + 2 z + 3 = 0 ; x + 2 y + 2 z - 17 = 0
D. x + 2 y + 2 z - 3 = 0 ; x + 2 y + 2 z + 17 = 0
Trong không gian Oxyz, cho mặt phẳng (P): x+2y+2z-10 = 0. Phương trình mặt phẳng (Q) song song với (P) và khoảng cách giữa hai mặt phẳng (Q) và (P) bằng 7 3 là
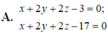
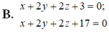
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng α :2x+y-2z+1=0; β :x-2y+2z+3=0 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là
A. Một mặt phẳng duy nhất
B. Một điểm duy nhất
C. Hai mặt phẳng phân biệt vuông góc với nhau
D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
![]()
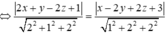
![]()
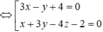
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.
Trong không gian Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P) có phương trình x - 2y + 2z + 1 = 0. Khoảng cách từ A đến mặt phẳng (P) là:
A. 8 3
B. - 8 3
C. 8 9
D. 8
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z - 1 = 0 và (Q): 3x + y + 2z - 3 = 0 là hai mặt phẳng có phương trình là:
A. x - 2y + z - 2 = 0 và 5x + 4y + 4z - 4 = 0
B. x - 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
C. x - 3y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
D. x + 2y + z - 2 = 0 và 5x + 4y + 3z - 4 = 0
Đáp án B
Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi:
d(M ; (P)) = d(M ; (Q))