Cho tam giác ABC, các đường phân giác BD và CE. Biết \(\frac{AE}{EB}=\frac{2}{3}\) ; \(\frac{AD}{DC}=\frac{2}{3}\)
Tính các cạnh của tam giác ABC, biết chu vi tam giác bằng 45 cm.

Những câu hỏi liên quan
Cho tam giác ABC có các đường phân giác BD và CE( \(D\in AC,E\in AB\)). Biết \(\frac{AD}{DC}=\frac{2}{3};\frac{AE}{EB}=\frac{5}{6}\), chu vi tam giác ABC là 45cm. Tính độ dài các cạnh của tam giác ABC.
Áp dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AB}{AD}=\frac{BC}{DC}\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{2}{3}\Rightarrow\frac{AB}{2}=\frac{BC}{3}\)(1)
Lại ap dụng định lý đường phân giác trong tam giác, ta được:
\(\frac{AC}{AE}=\frac{BC}{EB}\Rightarrow\frac{AC}{BC}=\frac{AE}{EB}=\frac{5}{6}\Rightarrow\frac{AC}{5}=\frac{BC}{6}\)(2)
Từ (1) và (2) suy ra \(\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{45}{15}=3\)
Vậy độ dài các cạnh của tam giác ABC lần lượt là 12;15;18 (cm)
Hình bạn tự vẽ nhé
Xét tam giác ABC có CE là đường phân giác của góc ACB (gt)
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}\)( tính chất đường phân giác trong của tam giác )
\(\Rightarrow\frac{AC}{BC}=\frac{5}{6}\)( Vì\(\frac{AE}{EB}=\frac{5}{6}\))
\(\Rightarrow6AC=5BC\)
Xét tam giác ABC có đường phân giác BD của góc ABC(gt)
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}\)( tích chất của đường phân giác trong của tam giác )
\(\Rightarrow\frac{AB}{BC}=\frac{2}{3}\)( Vì \(\frac{AD}{DC}=\frac{2}{3}\))
\(\Rightarrow3AB=2BC\)
Theo bài ra ta có: \(\hept{\begin{cases}6AC=5BC\\3AB=2BC\end{cases}}\)và \(AB+BC+CA=45\)
\(\Rightarrow\hept{\begin{cases}\frac{AC}{5}=\frac{BC}{6}\\\frac{AB}{4}=\frac{BC}{6}\end{cases}}\)
\(\Rightarrow\frac{AB}{4}=\frac{AC}{5}=\frac{BC}{6}=\frac{AB+AC+BC}{4+5+6}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}AB=3.4=12\left(cm\right)\\AC=3.5=15\left(cm\right)\\BC=3.6=18\left(cm\right)\end{cases}}\)
Vậy ...
+) Xét tam giác ABC có : CE là đường phân giác ( GT )
\(\Rightarrow\frac{AE}{EB}=\frac{AC}{BC}=\frac{5}{6}\)( T/c đường phân giác trong tam giác )
\(\Rightarrow5BC=6AC\)
Tương tự xét tam giác ABC có BD là phân giác ( GT )
\(\Rightarrow\frac{AD}{DC}=\frac{AB}{BC}=\frac{2}{3}\)
\(\Rightarrow2BC=3AB\)
Ta có :
\(\hept{\begin{cases}5BC=6AC\\2BC=3AB\end{cases}}\)(1) và \(AB+AC+BC=45\)( Do diện tích tam giác ABC = 45cm )
Từ ( 1 )
\(\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{3}=\frac{AB}{2}\end{cases}\Rightarrow\hept{\begin{cases}\frac{BC}{6}=\frac{AC}{5}\\\frac{BC}{6}=\frac{AB}{4}\end{cases}\Leftrightarrow}}\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}\)
Áp dụng TC của dãy tỉ số bằng nhau , ta có :
\(\frac{BC}{6}=\frac{AC}{5}=\frac{AB}{4}=\frac{BC+AC+AB}{6+5+4}=\frac{45}{15}=3\)
\(\Rightarrow\hept{\begin{cases}BC=18\\AC=15\\AB=12\end{cases}}\)
P/s : Bạn Châu sai chỗ nào zậy ?? k sai bừa !!
Xem thêm câu trả lời
Cho tam giác ABC, các đường phân giác BD và CE. Biết\(\frac{AD}{DC}=\frac{2}{3}\), \(\frac{EA}{Eb}=\frac{5}{6}\) Tính các cạnh tam giác ABC biết chu vi tam giác bằng 45cm .
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3 , EA/EB = 5/6 . Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
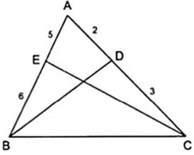
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
+ AB/BC = AD/DC = 2/3 = 4/6
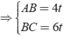 với t > 0
với t > 0
+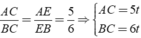
Theo giả thiết ta có: P A B C = A B + A C + B C = 15 t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 2
Bình luận (0)
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
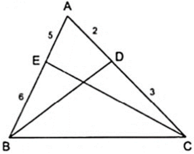
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
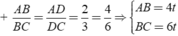 với t > 0
với t > 0
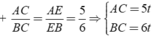
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường phân giác BD và CE. Biết AD/DC = 2/3, EA/EB = 5/6. Tính các cạnh của tam giác ABC, biết chu vi của tam giác là 45cm.
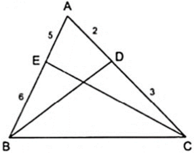
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
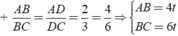 với t > 0
với t > 0
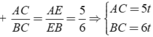
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )
Đúng 0
Bình luận (0)
Cho tam giác ABC. các đường phân giác BD và CE biết AD/DC=2/3; AE/EB5/6. Tính các cạnh của tam giác biết chu vi của nó bằng 45 cm.
CHO TAM GIÁC ABC, 3 ĐƯỜNG PHÂN GIÁC AD, BE, CF ĐỒNG QUI TẠI I. DỰA VÀO T/C ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC, EM CÓ ĐC NHỮNG TỈ LỆ THỨC NÀO? TÍNH\(\frac{AF}{BF}\cdot\frac{BD}{CD}\cdot\frac{CE}{AE}\)
Cho tam giác ABC,AB=8cm,BC=10cm,CA=6cm.Đường phân giác góc A và góc C cắt cạnh BC cà AB lần lượt ở D và E
a)Tính độ dài các đoạn thằng AE,AD,EB,DC
b)Trên cạnh BC lấy điểm K sáo cho BK=\(\frac{40}{7}\)cm.Chứng minh rằng 3 đường thẳng AK,BD,CE đồng quy
cho tam giác ABC trên cạnh AB láy điểm E sao cho AE bằng 2 EB trên cạnh AC lấy điểm D sao cho AD=1/3 CD các đoạn thẳng BD và CE cắt nhau tại F biết diên tích tam giác BÈ là 100cm2 tính dieebj tích tam giác ABC
CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn
Đúng 0
Bình luận (0)
Cho tam giác abc ,các đường phân giác BD và CE .C/mr BD+CE>\(\frac{3}{2}\)BC
giúp mk với















