Cho tam giác ABC , cho AD là đường phân giác trong của góc A. Chứng minh rằng: AD^2=AB.AC-DB.DC

Những câu hỏi liên quan
Cho tam giác ABC, AD là đường phân giác ngoài góc A . Chứng minh AD^2 = DB.DC - AB.AC?
Trên tia AD lấy điểm E sao cho ^BEA = ^BCA.
Khi đó ^BED = ^ACD và ^BDE = ^ADC nên hai tam giác BDE và ADC đồng dạng
suy ra BD/AD = DE/DC
suy ra AD.DE = DB.DC (1).
Gọi F là điểm đối xứng với C qua đường thẳng AD
vì AD là phân giác ^BAC nên F thuộc AB,
từ tính chất đối xứng suy ra ^DFA = ^DCA và AF = AC,
vì ^DCA = ^BCA = ^BEA nên ^DFA = ^BEA,
cùng với ^A chung nên hai tam giác DFA và BEA đồng dạng,
suy ra AD/AB = AF/AE = AC/AE, suy ra AD.AE = AB.AC (2).
Từ (2) và (1) theo vế thì có AD.(AE - DE) = AB.AC - DB.DC, suy ra AD^2 = AB.AC - DB.DC.
Đúng 0
Bình luận (0)
cho hỏi bài này và chứng minh theo tính chất của BĐT
cho tam giác ABC CD là giân giác của tam giác cm: CD^2
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC có AB=6cm ; AC=10cm ; BC=12cm . Vẽ đường phân giác AD của góc A . Trên tia đối của tia DA lấy điểm I sao cho góc ACI = góc BDA
a) Tính DB , DC
b) Chứng minh tam giác ACI đồng dạng với tam giác CDI
c) Chứng minh AD^2=AB.AC-DB.DC
a) DB?, DC?
Ta có:\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(tính chất đường phân giác)
⇒\(\dfrac{DB}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Mặt khác \(\dfrac{DB}{3}=\dfrac{DC}{5}\)
\(\dfrac{DB}{3}=\dfrac{DC}{5}=\dfrac{DB+DC}{3+5}=\dfrac{BC}{8}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{DB}{3}=\dfrac{3}{2}\\ \Rightarrow DB=\dfrac{3\times3}{2}=\dfrac{9}{2}=4.5\left(cm\right)\)
Và \(\dfrac{DC}{5}=\dfrac{3}{2}\\ \Rightarrow DC=\dfrac{3\times5}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Vậy DB=4,5(cm), DC= 7,5 cm
Đúng 2
Bình luận (0)
Cho tam giác ABC, đường phân giác AD. Chứng minh AD2 = AB.AC - DB.DC
Bạn tự vẽ hình nhé :))
Từ B kẻ tia Bx cắt AD tại E sao cho góc ABE = góc ADC.
\(\Delta AEB\)và \(\Delta ACD\)có: góc ABE = góc ADC (cách dựng) và góc BAE = góc DAC (gt)
\(\Rightarrow\)\(\Delta AEB\)đồng dạng \(\Delta ACD\)\(\Rightarrow\)\(\frac{AB}{AD}=\frac{AE}{AC}\)\(\Rightarrow\)\(AB.AC=AE.AD\)(1)
\(\Rightarrow\)góc BED = góc ACD.
\(\Delta ACD\)và \(\Delta BED\)có: góc ACD = góc BED (cmt) và góc ADC = góc BDE (đối đỉnh)
\(\Rightarrow\)\(\Delta ACD\)đồng dạng \(\Delta BED\)\(\Rightarrow\)\(\frac{DB}{AD}=\frac{DE}{DC}\)\(\Rightarrow\)\(DB.DC=DE.AD\)(2)
Lấy (1) - (2) vế theo vế ta được \(AB.AC-DB.DC=AD\left(AE-DE\right)\)\(\Leftrightarrow\)\(AD^2=AB.AC-DB.DC\)(đpcm).
Đúng 0
Bình luận (0)
Bài 2:
2cm x 3 = 6cm 2kg x 4 = 8kg
2cm x 5 = 10cm 2kg x 6 = 12kg
2dm x 8 = 16cm 2kg x 9 = 18kg
Bài 3:
Số bánh xe của 78 xe đạp là:
2 x 8 = 16 (bánh xe)
Đáp số: 16 bánh xe.
Bài 4: Hướng dẫn: Điền lần lượt từ trái sang phải vào các ô trống còn lại là: 12, 18, 20, 14, 10, 16, 4.
Bài 5:
Hướng dẫn: Điền lần lượt từ trái sang phải vào các ô trống các số là: 10, 14, 18, 20, 4.
Xem thêm tại: http://loigiaihay.com/bai-1-bai-2-bai-3-bai-4-bai-5-tiet-92luyen-tap-c114a15865.html#ixzz4bgUlUPRO
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC ( AB < AC), phân giác AD. Ở miền ngoài tam giác ABC vẽ tia Cx sao cho góc BCx bằng góc BAD. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:
a) tam giác ABD đồng dạng với tam giác ACI
b) AD bình phương = AB.AC - DB.DC
Cho tam giác ABC (AB<AC) đừơng phân giác AD (D thuộc BC). Trên tia đối cuả DA lấy điểm I sao cho góc ACI = góc BDA. Chứng minh rằng. a) -Tam giác ADB đồng dạng tam giác ACI -Tam giác ADB đồng dạng tam giác CDI
b) AD bình phương=AB.AC-DB.DC
Cho tam giác ABC (AB khác AC), phân giác AD. Trên nửa mặt phẳng bờ BC không chứa A vẽ góc BCx=góc BAD. Gọi E là giao điểm của Cx và AD. Chứng minh:
a) Tam giác ADB đồng dạng tam giác ACE
b) Tam giác ADB đồng dạng tam giác CDE
c) AD^2=AB.AC-DB.DC
cho tam giác ABC đường phân giác AD trên nửa mặt phẳng bờ BC không chứa A vẽ tia Cx sao cho ^BCx bằng ^A/2 hai tia Cx và AD cắt nhau tại E chứng minh rằng a)tam giác ABD đồng dạng tam giác CED b) tam giác ABD đồng dạng tam giác AED c) AB.AC=DB.DC=AD^2
Cho tam giác ABC có AB=6, AC=10, BC=12. Vẽ đường phân giác AD của góc BAC, trên tia đối tia DA lấy điểm I sao cho góc ACI=góc BDA.
a) Tính DB và DC
b) Chứng minh ∆ACI đồng dạng ∆CDI
c)Chứng minh AD^2=AB.AC - DB.DC
Cho tam giác ABC (AB AC), đường phân giác trong AD. Trên tia đối của tia DA lấy điểm I sao cho
A
C
I
^
B
D
A
^
.
Chứng minh:a)
Δ
A
B
D
∽
Δ
A
I
C
;
b)
Δ
A...
Đọc tiếp
Cho tam giác ABC (AB < AC), đường phân giác trong AD. Trên tia đối của tia DA lấy điểm I sao cho A C I ^ = B D A ^ . Chứng minh:
a) Δ A B D ∽ Δ A I C ; b) Δ A B D ∽ Δ C I D ;
c) A D 2 = A B . A C − D B . D C .
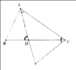
a) HS tự chứng minh.
b) HS tự chứng minh.
c) Từ a, suy ra AB.AC = AD.AI (1)
Từ b, suy ra BD.CD = AD.ID (2)
Từ (1) và (2), ta chứng minh được AD2 = AB.AC- DB.DC
Đúng 0
Bình luận (0)

















