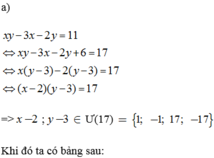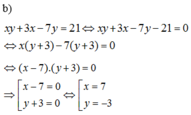Tìm x,y biết : (x+2y )(3x+7y)=216

Những câu hỏi liên quan
Tìm nghiệm nguyên dương của:
(x + 2y)(3x + 7y)=216
Tìm x, y biết :
3x + 2y = 7y - 3x và x - y = 10
\(3x+2y=7y-3x\)
\(\Leftrightarrow3x+3x=7y-2y\)
\(\Leftrightarrow6x=5y\)
\(\Leftrightarrow\frac{x}{5}=\frac{y}{6}\)và \(x-y=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{5}=\frac{y}{6}=\frac{x-y}{5-6}=\frac{10}{-1}=-10\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{5}=-1\\\frac{y}{6}=-1\end{cases}\Rightarrow\hept{\begin{cases}x=-1.5=-5\\y=-1.6=-6\end{cases}}}\)
Vậy \(x=-5;y=-6\)
Đúng 0
Bình luận (2)
\(3x+2y=7y-3x\)
\(3x+3x=7y-2y\)
\(6x=5y\Leftrightarrow\frac{x}{5}=\frac{y}{6}\)
TTheo t/c dãy tỉ số bằng nhau
\(\Rightarrow\frac{x}{5}=\frac{y}{6}=\frac{x-y}{5-6}=\frac{10}{-1}=-10\)
\(\Rightarrow x=-50;y=-60\)
Đúng 0
Bình luận (0)
\(3x+2y=7y-3x\)
\(\Rightarrow6x=5y\)(1)
Lại có: \(x-y=10\)
\(\Rightarrow x=10+y\)(2)
Thay (2) vào (1): \(\Rightarrow6\left(10+y\right)=60+6y=5y\)
\(\Rightarrow-y=60\Rightarrow y=-60\)
\(\Rightarrow5y=-60.5=-300=6x\)
\(\Rightarrow x=-50\)
Vậy \(x=-50;y=-60\)
Đúng 0
Bình luận (0)
tìm x,y,z biết :3x=2y,7y=5z và x-y+z=32
3x = 2y => x/2 = y/3 => x/10 = y/15 (1)
7y = 5z => y/5 = z/7 => y/15 = z/21 (2)
Từ (1) và (2) => x/10 = y/15 = z/21
Áp dụng tình chất của dãy tỉ số bằng nhau:
(tự làm nha)
Đúng 0
Bình luận (0)
Tìm x, y biết : 3x=2y , 7y=5z và x-y+z=32
\(3x=2y;7y=5z\) va x-y+z=32
\(\Rightarrow3x=2y=\frac{x}{2}=\frac{y}{3}\)
\(\Rightarrow7y=5z=\frac{y}{5}=\frac{z}{7}\)
\(\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{x}{2}=\frac{5y}{15};\frac{3y}{15}=\frac{z}{7}\Rightarrow\frac{x}{10}=\frac{y}{15};\frac{y}{15}=\frac{z}{21}\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x-y+z}{10-15+21}=\frac{32}{16}=2\)
Suy ra : \(\frac{x}{10}=2\Rightarrow x=2.10=20\)
\(\frac{y}{15}=2\Rightarrow y=2.15=30\)
\(\frac{z}{21}=3\Rightarrow z=3.21=63\)
Đúng 0
Bình luận (0)
3x=2y=>x/2=y/3=>x/10=y/15
7y=5z=>y/5=z/7=>y/15=z/21
=>x/10=y/15=z/21=x-y+z/10-15+21=32/16=2
=>x=20;y=30;z=42
vậy x=20;y=30;z=42
Đúng 2
Bình luận (0)
\(3x=2y;7y=5z\Rightarrow\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{x}{10}=\frac{y}{15};\frac{y}{15}=\frac{z}{21}\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x-y+z}{10-15+21}=\frac{32}{16}=2\)
suy ra:
\(\frac{x}{10}=2\Rightarrow x=2.10=20\)
\(\frac{y}{15}=2\Rightarrow y=2.15=30\)
\(\frac{z}{21}=2\Rightarrow z=2.21=42\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm x, y biết:
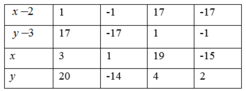
a) x y − 3 x − 2 y = 11
b) x y + 3 x − 7 y = 21
tìm x,y thuộc Z biết :
a) x . y + 3x - 7y = 21
b) x . y + 3x - 2y = 11
x.y + 3x - 2y = 11
=> x.y + 3x - 2y - 11 = 0
=> x.y + 3x - 2y - 6 - 5 = 0
=> x.(y+3) -2(y+3)- 5 = 0
=> (x-2)(y+3) = 5
tự tính nhé đến đây dễ rồi
Đúng 0
Bình luận (0)
x.y + 3x - 7y = 21
=> x.y + 3x -7y - 21 = 0
=> x( y+3) - 7(y+3) = 0
=> (x-7)(y+3) = 0
=>\(\orbr{\begin{cases}x-7=0\\y+3=0\end{cases}}\)
=> x= 7 hoặc y = -3
Đúng 0
Bình luận (0)
a, (x;y) = (2;-3)
b, (x;y) = (7;-3)
Ez game
Đúng 0
Bình luận (0)
Tìm x,y,z biết: 3x=2y,5x=7y và x-y+z=32
tìm x, y ,z biết 3x=2y, 7y=5z và x-y+z= 32
Tìm x;y;z biết:
3x = 2y; 7y =5z và x - y + z = 32
Tìm x, y, z bik 3x = 2y, 7y = 5z và x-y+z = 32
Ta có 3x=2y => x/2=y/3 <=> x/10 = y/15 (1)
7y = 5z => z/7 = y/5 <=> z/21 = y/15 (2)
Từ 1 và 2 ta suy ra x/10 = y/15 = z/21 = (x-y+z)/(10-15+21) = 32/16 = 2
Vậy x = 10*2 = 20
y = 15*2 = 30
z = 21*2 = 42
Đúng 0
Bình luận (0)
3x = 2y => x = (2/3)y (1)
7y = 5z => z =(7/5)y (2)
thay (1) và (2) vào x - y + z = 32 ta được :
(2/3)y - y + (7/5)y = 32
=> (2/3 -1 + 7/5)y = 32
=> (16/15)y = 32
=> y = 30
thay y = 30 vào (1) và (2) ta được x = 20 và z = 42
kl: x = 20 , y = 30 ,z = 42
Đúng 0
Bình luận (0)