Cho tam giác nhọn DEF có DE

Những câu hỏi liên quan
BT: Cho tam giác nhọn DEF có DH, HM, HN lần lượt là các đường cao của các tam giác DEF, HDF, HDE. Chứng minh DM*DF=DN*DE
cho 2 tam giác ABC và DEF có các góc đều nhọn và có: góc ABC=góc DEF ;góc BAC =góc EDF;AB=3.DE....chứng minh rằng bán kình đường trong ngoại tiếp tam giác ABC=3 lần bán kính đường trong ngoại tiếp tam giác DEF...
Gọi ( O;R ) , ( I ;r ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF};\widehat{BAC}=\widehat{EDF}\)) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ACB},\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)( hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OB\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
\(ID=IE\left(=r\right)\Rightarrow\Delta IDE\)cân tại I
Do đó Tam giác OAB ~ Tam giác IDE \(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\) ( đpcm)
Đúng 0
Bình luận (0)
Gọi ( O; R ), ( I; R ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF;}\widehat{BAC}=\widehat{EDF}\) ) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ABC}=\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)(hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OA\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
Do đó Tam giác OAB ~ Tam giác IDE\(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\left(đpcm\right)\)
Rất vui vì giúp đc bạn <3
Đúng 0
Bình luận (0)
cho tam giác abc & def cs các góc đều nhọn và cs góc abc=def; bac=edf; ab=3.de... chứng minh rằng bán kính đường tròn ngoại tiếp tam giác def...
Bài 1:
Cho tam giác DEF nhọn. DE<DF, lấy M thuộc cạnh DE, N thuộc cạnh DF sao cho MN//EF. Cho biết DM=2cm, DN=3,5cm. Tính NF.
Bài 2:
Cho tam giác DEF nhọn, DE<DF. Lấy K thuộc cạnh DE, I thuộc cạnh DF sao cho KI//EF. Cho biết DK=3cm, KE=1cm, DI=4,2cm. Tính IF.
1) tam giác DEF có MN//EF
=> \(\frac{DM}{ME}=\frac{DN}{NF}=>\frac{2}{2}=\frac{3,5}{NF}=>NF=\frac{3,5.2}{2}=3,5cm\)
2)tam giasc DEF cos KI//EF
=>\(\frac{DK}{KE}=\frac{DI}{IF}=\frac{3}{1}=\frac{4,2}{IF}=IF=\frac{1.4,2}{3}=1,4cm\)
Cho tam giác DEF có 3 góc nhọn (DEDF), kẻ đường cao DH của tam giác DEF. Gọi M,N,Q lần lượt là trung điểm của DE, DF, EF. Gọi K là điểm đối xứng với D qua Q, A là điểm đối xứng với H qua N.a) Chứng minh tứ giác DEKF là hình bình hành.b)Chứng minh tứ giác ADHF là hình chữ nhật. Hỏi tam giác DEF có thêm điều kiện gì để tứ giác ADHF là hình vuông.c)Chứng minh MNQH là hình thang cân.d) Giả sử tam giác DEF có góc DFE 45 độ. Gọi G là trung điểm của DA, MN cắt DH tại I, AI cắt FG tại S. Chứng minh góc...
Đọc tiếp
Cho tam giác DEF có 3 góc nhọn (DE<DF), kẻ đường cao DH của tam giác DEF. Gọi M,N,Q lần lượt là trung điểm của DE, DF, EF. Gọi K là điểm đối xứng với D qua Q, A là điểm đối xứng với H qua N.
a) Chứng minh tứ giác DEKF là hình bình hành.
b)Chứng minh tứ giác ADHF là hình chữ nhật. Hỏi tam giác DEF có thêm điều kiện gì để tứ giác ADHF là hình vuông.
c)Chứng minh MNQH là hình thang cân.
d) Giả sử tam giác DEF có góc DFE = 45 độ. Gọi G là trung điểm của DA, MN cắt DH tại I, AI cắt FG tại S. Chứng minh góc HDS= góc HSD.
Giúp mik bài hình này với<3
Chọn câu đúng
A.
Tam giác DEF có DE = DF thì tam giác DEF cân tại E
B.
Tam giác DEF có DE = DF thì tam giác DEF cân tại F
C.
Tam giác DEF có DE = DF thì tam giác DEF cân tại D
D.
Tam giác DEF có FE = DF thì tam giác DEF cân tại D
Xem thêm câu trả lời
Cho tam giác nhọn DEF có DE<DF, tia phân giác của góc DEF cắt DF tại I. Lấy K trên EF sao cho ED=EK.
a) Chứng minh tam giác DEI = tam giác KEI.
b) Gọi H là giao điểm của ED và KI. Chứng minh DH=KF.
(Có hình nữa càng tốt nha các bạn. Thank you very much!)
Cho tam giác ABC nhọn có 3 đường cao DH , EI , FK cắt nhau tại O
a , CMR : tam giác DKF đồng dạng với tam giác DIE
và DK . DE = DF . DI
b , CMR : tam giác DKI đồng dạng với tam giác DFE
c , CMR : góc FIH = DEF , IE là tia phân giác của góc KIH
d , Cmr : EK . ED + FI . FD = EK2
Sửa đề: Cho ΔDEF nhọn
a: Xét ΔDKF vuông tại K và ΔDIE vuông tại I có
\(\widehat{KDF}\) chung
Do đó: ΔDKF~ΔDIE
=>\(\dfrac{DK}{DI}=\dfrac{DF}{DE}\)
=>\(DK\cdot DE=DI\cdot DF\)
b: ta có: \(\dfrac{DK}{DI}=\dfrac{DF}{DE}\)
=>\(\dfrac{DK}{DF}=\dfrac{DI}{DE}\)
Xét ΔDKI và ΔDFE có
\(\dfrac{DK}{DF}=\dfrac{DI}{DE}\)
\(\widehat{KDI}\) chung
Do đó: ΔDKI~ΔDFE
c: Xét ΔFIE vuông tại I và ΔFHD vuông tại H có
\(\widehat{HFD}\) chung
Do đó: ΔFIE~ΔFHD
=>\(\dfrac{FI}{FH}=\dfrac{FE}{FD}\)
=>\(\dfrac{FI}{FE}=\dfrac{FH}{FD}\)
Xét ΔFIH và ΔFED có
\(\dfrac{FI}{FE}=\dfrac{FH}{FD}\)
\(\widehat{EFD}\) chung
Do đó: ΔFIH~ΔFED
=>\(\widehat{FIH}=\widehat{FED}\)
d:
Sửa đề: \(EK\cdot ED+FI\cdot FD=EF^2\)
Xét ΔEKF vuông tại K và ΔEHD vuông tại H có
góc KEF chung
Do đó: ΔEKF~ΔEHD
=>\(\dfrac{EK}{EH}=\dfrac{EF}{ED}\)
=>\(EK\cdot ED=EF\cdot EH\)
Ta có: \(\dfrac{FI}{FE}=\dfrac{FH}{FD}\)
=>\(FI\cdot FD=FH\cdot FE\)
\(EK\cdot ED+FI\cdot FD\)
\(=EF\cdot EH+FH\cdot EF=EF^2\)
Đúng 2
Bình luận (1)
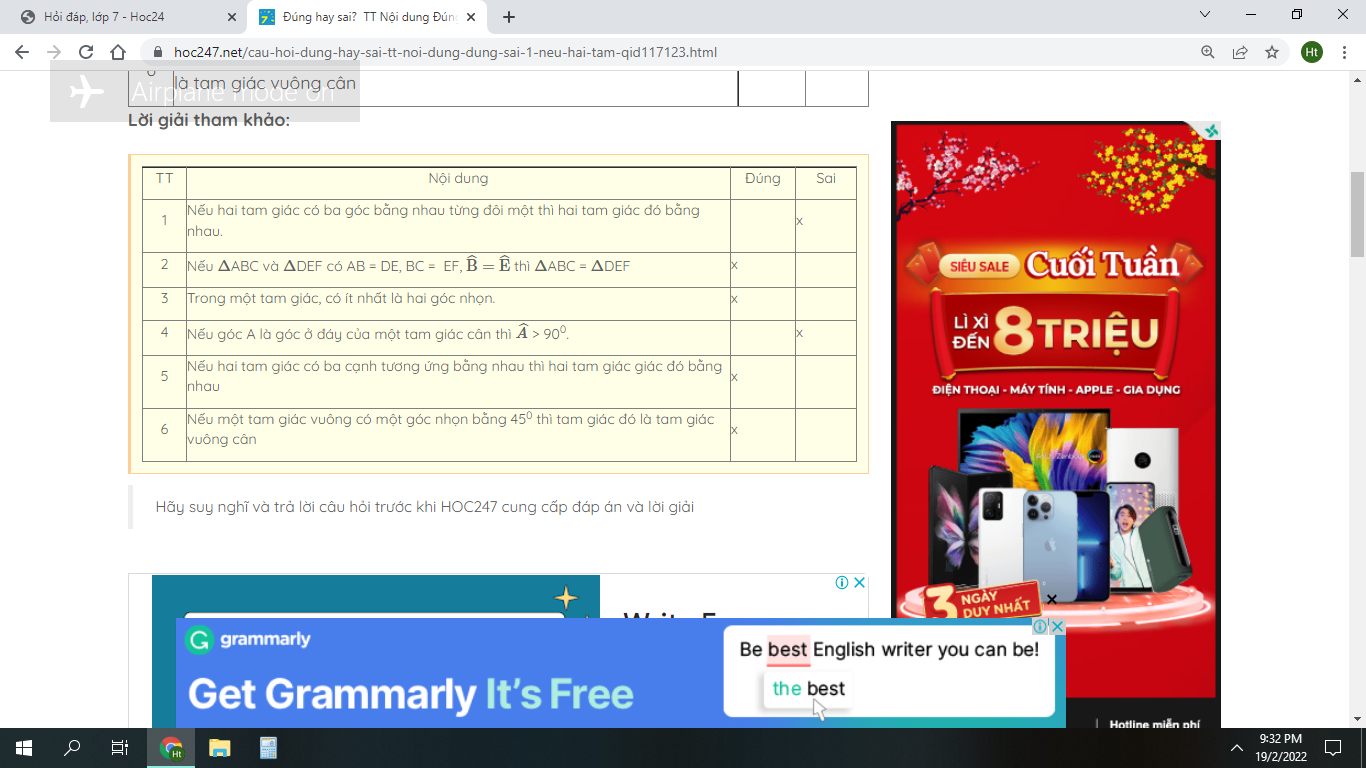
Bài 2: Đúng hay sai?TTNội dungĐúngSai1Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. 2Nếu ABC và DEF có AB DE, BC EF, thì ABC DEF 3Trong một tam giác, có ít nhất là hai góc nhọn. 4Nếu góc A là góc ở đáy của một tam giác cân thì 900. 5Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau 6Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân
Đọc tiếp
Bài 2: Đúng hay sai?
TT | Nội dung | Đúng | Sai |
1 | Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. |
|
|
2 | Nếu ABC và DEF có AB = DE, BC = EF, thì ABC = DEF |
|
|
3 | Trong một tam giác, có ít nhất là hai góc nhọn. |
|
|
4 | Nếu góc A là góc ở đáy của một tam giác cân thì > 900. |
|
|
5 | Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau |
|
|
6 | Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân |
|
|
TT | Nội dung | Đúng | Sai |
1 | Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. |
| x |
2 | Nếu ABC và DEF có AB = DE, BC = EF, thì ABC = DEF | x |
|
3 | Trong một tam giác, có ít nhất là hai góc nhọn. | x |
|
4 | Nếu góc A là góc ở đáy của một tam giác cân thì > 900. |
| x |
5 | Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau | x |
|
6 | Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân Đúng |
Chúc em học giỏi
Đúng 0
Bình luận (1)