Tính góc C1 và góc C2

Những câu hỏi liên quan
cho hình vẽ biết c//d và b 1 = 85 độ c4 = 105 độ tính các góc a1,a2,a3,a4,b2,b3,b4,c1,c2,c3,d1,d2,d3,d4
cho hình vẽ,biết A1=B1=85 C1=120 a) chứng minh a//b b) Tính C2 và D1 c) vẽ tia phân giác Cx của góc cắt ACD tại I .Tính góc CDI
Cho hình vẽTính số đo các góc C1 ,C2?c,Vẽ lần lượt là các tia phân giác của các góc C1 ,C2tính số đo của góc xCy a b C D 80 độ 1 2
Đọc tiếp
Cho hình vẽ
Tính số đo các góc C1 ,C2?
c,Vẽ lần lượt là các tia phân giác của các góc C1 ,C2
tính số đo của góc xCy
Cho hình vẽ, có: Ax song song By song song Cz. a) So sánh góc A1 và góc C1. b) Tính góc C1 + góc CAx. c) góc C2 + góc CBy bằng ?. d) Nếu AB vuông góc với By thì AB có vuông góc Ax không ? AB có vuông góc với Cz không ? Vì sao
Cho hình vẽ: a c/m AB //CDb c/m AD//BCc tính góc C1;C2;C3 A B C D 1 2 3 1 1 1 110 110 70 O O O
Đọc tiếp
Cho hình vẽ:
a c/m AB //CD
b c/m AD//BC
c tính góc C1;C2;C3
các đường thẳng Ax,By,Cz song song với nhau như hình vẽ: A B x y z C 1 1 2 a) Các góc A1 ,C1 có bằng nhau ko ? Vì sao?b) tính C1 +CAxc) tính C2 +CByd) tính CAx + CBy +ACB e) nếu ABperp By thì AB có vuông góc với Ax và Cz ko ? Vì sao ?
Đọc tiếp
các đường thẳng Ax,By,Cz song song với nhau như hình vẽ:
a) Các góc A1 ,C1 có bằng nhau ko ? Vì sao?
b) tính C1 +CAx
c) tính C2 +CBy
d) tính CAx + CBy +ACB
e) nếu AB\(\perp\) By thì AB có vuông góc với Ax và Cz ko ? Vì sao ?
Bài 11.Biết a // b; góc CAM 450; góc MBD 400 a) Tính góc AMB b) Biết góc C1 C2. Chứng minh c perp b.
Đọc tiếp
Bài 11.Biết a // b; góc CAM = 450; góc MBD = 400
a) Tính góc AMB
b) Biết góc C1 = C2. Chứng minh c \(\perp\) b.
a) Kẻ Mz//a//b( Mz thuộc nửa mặt phẳng bờ MB không chứa điểm D)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{AMz}=\widehat{CAM}=45^0\\\widehat{BMz}=\widehat{MBD}=40^0\end{matrix}\right.\)(so le trong)
\(\Rightarrow\widehat{AMB}=\widehat{AMz}+\widehat{BMz}=45^0+40^0=85^0\)
b) Ta có: \(\widehat{C_1}=\widehat{C_2}=180^0:2=90^0\)(kề bù)
\(\Rightarrow c\perp a\)
Mà a//b
\(\Rightarrow c\perp b\)
Đúng 1
Bình luận (0)
a. Xét dấu của biểu thức f(x) 2x(x+2)-(x+2)(x+1)b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y 2x(x+2) ( C1 ) và y (x+2)(x+1)(C2)Tính tọa độ giao điểm A và B của (C1) và (C2).c. Tính các hệ số a, b, c để hàm số y ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Đọc tiếp
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2
Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.
Vậy:
+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)
+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)
+ f(x) = 0 nếu x = -2 hoặc x = 1.
b)
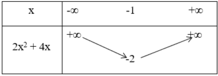
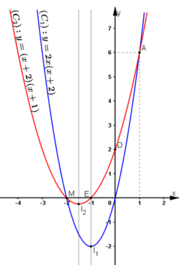
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:
+ Tập xác định: D = R
+ Đỉnh I1( -1; -2)
+ Trục đối xứng: x = -1
+ Giao điểm với trục tung tại gốc tọa độ.
+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).
+ Bảng biến thiên:
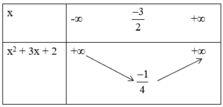
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:
+ Tập xác định D = R.
+ Đỉnh 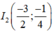
+ Trục đối xứng: x = -3/2
+ Giao với trục tung tại D(0; 2)
+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)
+ Bảng biến thiên
* Đồ thị:
* Tìm tọa độ giao điểm:
Cách 1: Dựa vào đồ thị hàm số:
Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)
Cách 2: Tính:
Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:
2x(x + 2) = (x + 2)(x + 1)
⇔ (x + 2).2x – (x + 2)(x + 1) = 0
⇔ (x + 2).(2x – x – 1) = 0
⇔ (x + 2).(x – 1) = 0
⇔ x = -2 hoặc x = 1.
+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)
+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).
c)
+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)
⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c
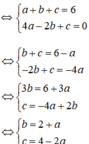
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:
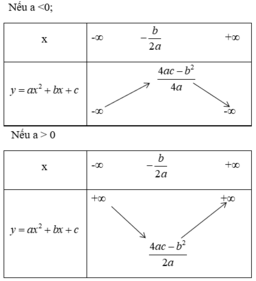
Nhận thấy y đạt giá trị lớn nhất bằng 8
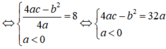
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:
4.a.(4 – 2a) – (2 + a)2 = 32a
⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a
⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0
⇔ -9a2 - 20a - 4 = 0
⇔ a = -2 hoặc a = -2/9.
Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8
Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số 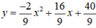
Đúng 1
Bình luận (0)
C1: Biết 2 lần góc A bằng 3 lần góc B và góc A - góc B = 30 độ. Tính các góc của tam giác ABC
C2: Cho tam giác ABC, góc B>góc C, đường phân giác góc ngoài BA của A cắt tia CB tại A
a) Chứng minh góc AEB = B-C phần 2
b) Tính số đo góc B,góc C của tam giác ABC, biết góc A=60 độ và góc AEB=15 độ
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
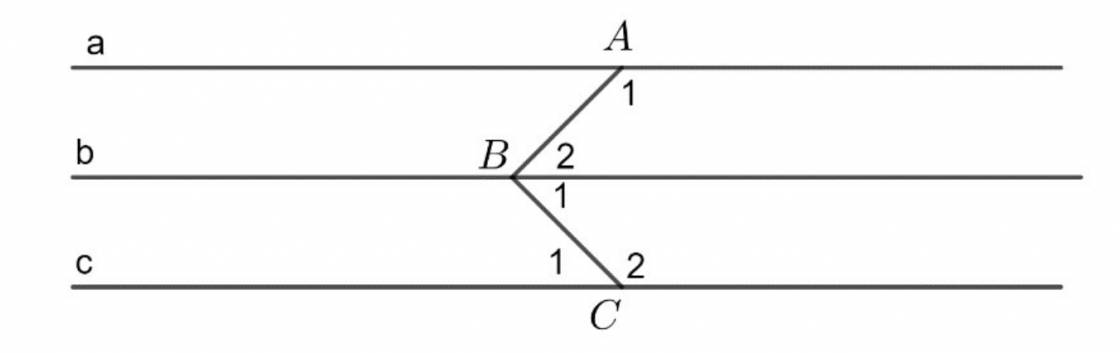
Cho hình vẽ dưới dây, biết a // b // c và B1 = 600, A1 = 1400. Hãy tính số đo các góc: C1, C2 và ABC.