Áp dụng quy tắc về căn thức bậc hai của một tích, hãy rút gọn biểu thức:
a) $\sqrt{9x^4}$;
b) $\sqrt{3a^3} \cdot \sqrt{27a}$ với a > 0.
Những câu hỏi liên quan
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 40
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 5
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 52 . 13
52 . 13 = 4 . 13 . 13 = 2 . 13 2 = 2 . 13 = 26
Đúng 0
Bình luận (0)
Áp dụng quy tắc nhân các căn thức bậc hai, hãy tính: 2 . 162
2 . 162 = 2 . 2 . 81 = 2 . 9 2 = 2 . 9 = 18
Đúng 0
Bình luận (0)
Áp dụng quy tắc chia hai căn bậc hai , hãy tính :
\(\frac{\sqrt{8^2}}{\sqrt{4^{5.}}\sqrt{2^3}}\)
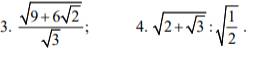áp dụng quy tắc chia căn bậc hai, hãy tính
\(3,\dfrac{\sqrt{9+6\sqrt{2}}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3\left(3+2\sqrt{2}\right)}}{\sqrt{3}}\)
\(=\dfrac{\sqrt{3}.\sqrt{3+2\sqrt{2}}}{\sqrt{3}}\)
\(=\sqrt{3+2\sqrt{2}}\)
\(=\sqrt{\sqrt{2^2}+2\sqrt{2}+1}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)
\(4,\sqrt{2+\sqrt{3}}:\sqrt{\dfrac{1}{2}}\)
\(=\sqrt{2+\sqrt{3}}:\dfrac{1}{\sqrt{2}}\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2}\)
\(=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\sqrt{3^2}+2\sqrt{3}+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)}^2\)
\(=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)
Đúng 3
Bình luận (0)
Áp dụng quy tắc chia hai căn bậc hai, hãy tính: 2300 23
Áp dụng quy tắc chia hai căn bậc hai, hãy tính: 12 , 5 0 , 5
Áp dụng quy tắc chia hai căn bậc hai, hãy tính: 6 150
Áp dụng quy tắc chia hai căn bậc hai, hãy tính: 192 12