Tự vẽ hình nhé

a) Gọi giao điểm cùa GD và BC là O 

=> OB = OC (do tam giác BAC cân tại A và AD là đường cao)

Tứ giác BGCD: (chỗ này sử dụng dấu hiệu 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường) 

=> tứ giác BGCD là hình thoi

b) Để BGCD là hình vuông thì BGC^ = 90o  <=> BM _|_ CN 

Vậy BGCD là hình vuông <=> tam giác ABC có 2 đường trung tuyến còn lại vuông góc với nhau

bài nhà cô loan à việt mai chữa bài không cần làm đâu

Bạn tự vẽ hình nhé. Mình chỉ có thể giải cho bạn câu a thui

Gọi E là giao điểm của GD và BC

a, Vì D đối xứng với G qua BC => GD vuông góc với BC và GE=ED

Ta C/m : A,G,D thẳng hàng

Xét tam giác ABC có: BM và CN là đường trung tuyến

                            => G là trọng tâm của tam giác ABC

                            => AG cũng là đường trung tuyến

                            => A,G,D thẳng hàng

Xét tam giác ABC cân tại A có: AE là đường cao => AE cũng là đường trung tuyến => BE=CE

Xét tứ giác BGCD có: đường chéo BC và GD cắt nhau tại trung điểm E

                                   GD vuông góc với BC

                             => BGCD là hình thoi

Mình chưa chắc chắn lắm về cách giải.  

Hình vẽ của mình không được chuẩn cho lắm thông cảm nha

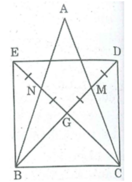
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G

Suy ra: G là trọng tâm của ∆ ABC .

⇒ GB = 2GM (tính chất đường trung tuyến)

GC = 2GN (tính chất đường trung tuyến)

Điểm D đối xứng với điểm G qua điểm M

⇒ MG = MD hay GD = 2GM

Suy ra: GB = GD (l)

Điểm E đối xứng với điểm G qua điểm N

⇒ NG = NE hay GE = 2GN

Suy ra: GC = GE (2)

Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Xét  ∆ BCM và  ∆ CBN, có: BC cạnh chung

∠ (BCM) =  ∠ (CBN) (tính chất tam giác cân)

CM = BN (vì AB = AC)

Suy ra:  ∆ BCM = ∆ CBN (c.g.c)

⇒  ∠ (MBC) =  ∠ (NCB) ⇒  ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE

Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.

a)

Xét tứ giác MNPQ có 

G là trung điểm của đường chéo MP(gt)

G là trung điểm của đường chéo NQ(gt)

Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)

b) 

Xét ΔABC có 

BM là đường trung tuyến ứng với cạnh AC(gt)

CN là đường trung tuyến ứng với cạnh AB(gt)

BM cắt CN tại G(gt)

Do đó: G là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)

Suy ra: \(MG=\dfrac{1}{3}MB;BG=\dfrac{2}{3}MB;NG=\dfrac{1}{3}NC;CG=\dfrac{2}{3}NC\)(1)

Ta có: G là trung điểm của MP(gt)

nên MG=GP

mà \(MG=\dfrac{1}{3}MB\)

nên \(MG=GP=\dfrac{1}{3}MB\)

Ta có: MG+GP=MP(G nằm giữa M và P)

nên \(MP=\dfrac{1}{3}MB+\dfrac{1}{3}MB=\dfrac{2}{3}MB\)(1)

Ta có: G là trung điểm của NQ(gt)

nên \(GN=GQ=\dfrac{1}{3}NC\)

Ta có: NG+GQ=NQ(G là trung điểm của NQ)

nên \(NQ=\dfrac{1}{3}NC+\dfrac{1}{3}NC=\dfrac{2}{3}NC\)(2)

Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)

\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)

mà AB=AC(ΔBAC cân tại A)

nên AN=NB=AM=MC

Xét ΔAMB và ΔANC có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAM}\) chung

AM=AN(cmt)

Do đó: ΔAMB=ΔANC(c-g-c)

Suy ra: BM=CN(hai cạnh tương ứng)(3)

Từ (1), (2) và (3) suy ra NQ=MP

Hình bình hành MNPQ có NQ=MP(cmt)

nên MNPQ là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)