từ A ngoài đường tròn (O, R) vẽ cát tuyến ADE ( D và E thuộc (O) và D nằm giữa A , E). Đường thẳng qua D vuông góc OB cắt BC, BE tại H, K. Vẽ OM vuông góc AE tại M. a) Chứng minh 4 điểm B, M,O , C thuộc 1 đường tròn

Những câu hỏi liên quan
từ điểm A nằm ngoài đường tròn (O;R) , dựng các tiếp tuyến AB,AC và cát tuyến ADE (D,E thuộc (O) và D nằm giữa A,E ). đường thẳng qua D vuông góc với OB cắt BC,BE lần lượt tại H,K . vẽ OI vuông góc với AE tại I.gọi S là giao điểm của BC và AD . 1/AD+1/AE=2/AS
Cho điểm A nằm ngoài đường tròn (O,R). Vẽ AB, AC là các tiếp tuyến của đường tròn (O) (B, C là các tiếp điểm). Vẽ cát tuyến ADE của đường tròn O ( D nằm giữa A và E). Các tiếp tuyến tại D và E của (O) cắt nhau tại K, OA cắt Bc tại H.
a) Chứng minh KH vuông góc với OA; K, B, C thẳng hàng.
b) AO cắt (O) tại M, N ( M nằm giữa O, H). Chứng minh KH, DN, EM đồng quy
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếpb) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD MH.ANCâu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CACB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.a) C/m: MO...
Đọc tiếp
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.
a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếp
b) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD= MH.AN
Câu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CA=CB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.
a) C/m: MOCD là hình bình hành
b) Vẽ đường tròn tâm E bán kính EA cắt (O) tại điểm thứ 2 là N. Kẻ EF vuông góc với AC, EF cắt AN tại I, cắt (O) tại điểm thứ 2 là K; EB cắt AN tại H. C/m: BHIK nội tiếp.
Câu 3: Cho (O;R). Từ điểm S nằm ngoài đường tròn sao cho SO=2R. Vẽ tiếp tuyến SA,SB (A,B là tiếp tuyến). Vẽ cát tuyến SDE (D nằm giữa S và E), điểm O nằm trong góc ESB. Từ O kẻ đường vuông góc với OA cắt SB tại M. Gọi I là giao điểm của OS và (O).
a) C/m: MI là tiếp tuyến của (O)
b) Qua D kẻ đường vuông góc với OB cắt AB tại H và EB tại K. C/m: H là trung điểm của DK.
Từ điểm A ở ngoài đường tròn (O;R) dựng các tiếp tuyến AB, AC và cát tuyến ADE (D,E thuộc (O) và D nằm giữa A,E). Đường thẳng qua D vuông góc với OB cắt BC, BE lần lượt tại H và K. Vẽ OI vuông góc với AE tại I.a) Chứng minh rằng tứ giác OIBC nội tiếp được đường tròn. (đã xong)b) Chứng minh rằng IA là tia phân giác góc BIC. (đã xong)c) Gọi S là giao điểm của BC và AD. Chứng minh rằng 2/AS 1/AD + 1/AE
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O;R) dựng các tiếp tuyến AB, AC và cát tuyến ADE (D,E thuộc (O) và D nằm giữa A,E). Đường thẳng qua D vuông góc với OB cắt BC, BE lần lượt tại H và K. Vẽ OI vuông góc với AE tại I.
a) Chứng minh rằng tứ giác OIBC nội tiếp được đường tròn. (đã xong)
b) Chứng minh rằng IA là tia phân giác góc BIC. (đã xong)
c) Gọi S là giao điểm của BC và AD. Chứng minh rằng 2/AS = 1/AD + 1/AE
Qua điểm A nằm bên ngoài đường tròn 0, kẻ các tiếp tuyến AB, AC và cát tuyến ADE không đi qua tâm O (D, E thuộc đường tròn (O) và D nằm giữa AE). Vẽ OI vuông góc AE tại I a) cm: tứ giác OIBA nội tiếp b) cm: AD. AE = AC² c) Vẽ BC cắt OA tại K. cm: góc AKD = góc AEO cảm ơn mn
a: Xét tứ giác OIBA có \(\widehat{OIA}=\widehat{OBA}=90^0\)
nên OIBA là tứ giác nội tiếp
b: Xét ΔACD và ΔAEC có
\(\widehat{ACD}=\widehat{AEC}\)
\(\widehat{DAC}\) chung
Do đó: ΔACD\(\sim\)ΔAEC
SUy ra: AC/AE=AD/AC
hay \(AC^2=AE\cdot AD\left(1\right)\)
c: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
Xét ΔOCA vuông tại C có CK là đường cao
nên \(AK\cdot AO=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AO=AD\cdot AE\)
hay AK/AE=AD/AO
Xét ΔAKD và ΔAEO có
AK/AE=AD/AO
góc KAD chung
DO đó: ΔAKD\(\sim\)ΔAEO
Suy ra: \(\widehat{AKD}=\widehat{AEO}\)
Đúng 5
Bình luận (0)
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểma/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường trònb/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE AB2c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DEmọi người giúp mik với ạ
Đọc tiếp
Từ điếm A ở ngoài đường tròn (O;R) vẽ các tiếp tuyến AB,AC đến (O) với B,C là các tiếp điểm
a/ Chứng minh OA vuông góc BC tại H và tứ giác OBAC nội tiếp đường tròn
b/ Từ A vẽ cát tuyến ADE (không qua O) cắt (O) tại D và E (D nằm giữa A và E). Chứng minh: AD.AE= AB2
c/ Vẽ dây cung BM song song với DE. Gọi giao điểm của CM và DE là i. Chứng minh i trung điểm DE
mọi người giúp mik với ạ
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
hay OA⊥BC(đpcm)
Đúng 1
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O,R) vẽ các tiếp tuyến AB,AC và các tuyến ADE(D và E thuộc (o) và D nằm giữa A và E ).Đường thẳng qua D vuông góc vs OB cắt BC , BE lần lượt tại H và K. Vẽ OI vuông góc vs AE tại I A) CM rằng 4 điểm B,I,O,C cùng thuộc một đường tròn b) cm IA là phân giác góc BIC c) gọi S là giao điểm của BC và AD. cm AC2 AD. AE và tứ giác IHDC nội tiếp d) cm frac{1}{AD}+frac{1}{AE}frac{2}{AS}
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O,R) vẽ các tiếp tuyến AB,AC và các tuyến ADE(D và E thuộc (o) và D nằm giữa A và E ).Đường thẳng qua D vuông góc vs OB cắt BC , BE lần lượt tại H và K. Vẽ OI vuông góc vs AE tại I
A) CM rằng 4 điểm B,I,O,C cùng thuộc một đường tròn
b) cm IA là phân giác góc BIC
c) gọi S là giao điểm của BC và AD. cm AC2 = AD. AE và tứ giác IHDC nội tiếp
d) cm \(\frac{1}{AD}+\frac{1}{AE}=\frac{2}{AS}\)
bạn cần đáp án của câu này nữa không, mình post
Đúng 0
Bình luận (0)
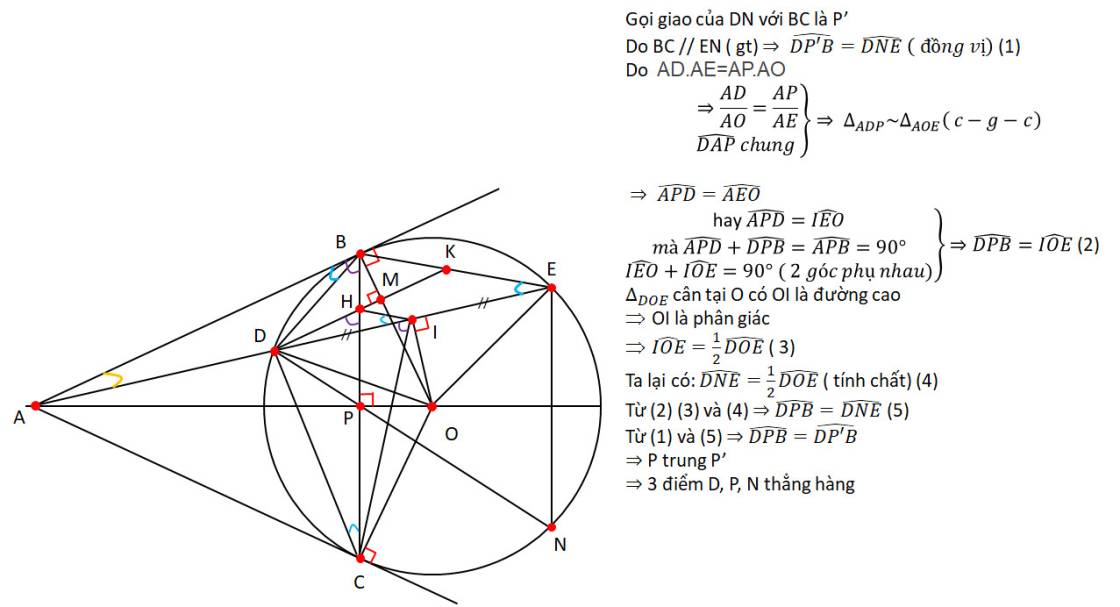
Từ điểm A nằm ngoài (O) dựng các tiếp tuyến AB,AC tới dg tròn và cát tuyến ADE (B thuộc cung nhỏ DE;D nằm giữa A và E ). Đường thẳng qua D vg với OB cắt BC,BE lần lượt tại H,K . vẽ OI vg với AE tại I . GỌI P là giao của AO và BCa) chứng minh tứ giác AIOC nội tiếpb) chứng minh AD.AEAP.AOc) chứng minh KDI BAE và tứ giác IHDC nội tiếpd) kẻ dây EN//BC chứng minh 3 điểm D,P,N thẳng hàng
Đọc tiếp
Từ điểm A nằm ngoài (O) dựng các tiếp tuyến AB,AC tới dg tròn và cát tuyến ADE (B thuộc cung nhỏ DE;D nằm giữa A và E ). Đường thẳng qua D vg với OB cắt BC,BE lần lượt tại H,K . vẽ OI vg với AE tại I . GỌI P là giao của AO và BC
a) chứng minh tứ giác AIOC nội tiếp
b) chứng minh AD.AE=AP.AO
c) chứng minh KDI =BAE và tứ giác IHDC nội tiếp
d) kẻ dây EN//BC chứng minh 3 điểm D,P,N thẳng hàng
a: góc AIO+góc ACO=180 độ
=>AIOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AP*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AP*AO
Đúng 0
Bình luận (0)
https://www.youtube.com/watch?v=HQsO2vLFaBw
BẠN THAM KHẢO BÀI NÀY NHÉ
Đúng 0
Bình luận (0)
Cho điểm A nằm ngoài đường tròn. Vẽ cấc tiếp tuyến AB, AC (B,C) là các tiếp điểm. Vẽ cát tuyến ADE đến đường tròn (O) ; D nằm giữa A và E ; tia AD nằm trong góc OAB . Gọi H là giao của OA và BC . Đuongwf thẳng qua O vuông góc với DE tại K cắt tiế tuyến tại D của (o) tại M.a, Chứng minh OA vuông góc BC; ME là tiếp tuyến của (o)b, Gọi I là giao của MB và AD. Chứng minh MH vuông góc OA; OI vuông góc AM
Đọc tiếp
Cho điểm A nằm ngoài đường tròn. Vẽ cấc tiếp tuyến AB, AC (B,C) là các tiếp điểm. Vẽ cát tuyến ADE đến đường tròn (O) ; D nằm giữa A và E ; tia AD nằm trong góc OAB . Gọi H là giao của OA và BC . Đuongwf thẳng qua O vuông góc với DE tại K cắt tiế tuyến tại D của (o) tại M.
a, Chứng minh OA vuông góc BC; ME là tiếp tuyến của (o)
b, Gọi I là giao của MB và AD. Chứng minh MH vuông góc OA; OI vuông góc AM