cho hình bình hanh abcd , ab =a bc = b ac = m . gọi i là giao điểm của 2 đường chéo ac và bd , tính số đo góc aib ??

Những câu hỏi liên quan
Cho hình bình hanh ABCD, hai đường chéo AC và BD cắt nhau taijO. Biết AC=2. AB, gọi E là trung điểm AO
a) tính BE/BC
b) Gọi M là trung điểm BC. Chứng minh EM vuông góc vs BD
cho hình thang cân ABCD (AB // CD) I là giao điểm hai đường chéo AC và BD , góc AIB = 60' gọi B' , C' là hình chiếu của B và C trên AC và BD.
a) chứng minh B' C' = 1/2 BC
b)Gọi E là trung điểm BC,chứng minh tam giác B'C'E đều
1. Cho hình thang ABCD có góc A=góc D=90độ. AC⊥Bd tại I. C/m:
a.ABD~DAC
b. Gọi E là hình chiếu của b xuống DC và BO=OD. C/m e điểm O,E,A thẳng hàng
c.Tỉ số diên tích AIB, DIC
2.Cho hình thang cân ABCD có AB//CD, AB<AC, đường chéo BD⊥cạnh bên BC, vẽ đường cao BH
a.BDC~HBC
b.Cho BC=15 cm, DC=25 cm. tính HC,HD
c.diện tích ABCD
Cho hình thang ABCD ( AB//CD), AB= BC, BC vuông góc BD
a) CMR : AC vuông góc AD
b) tính số đo các góc hình thang
Pc) Gọi O là giao điểm của 2 đường chéo. CMR: điểm Ở cách 2 cạnh bên và đáy lớn
a) vì ABCD: hthang=>AD=BC; góc DAB= ABC (1) ; AC=BD
Xét tam giác DAB và CBA có:
AB: chung
góc DAB=ABC
AD=BC
=> DAB=CBA(c.g.c)
=> góc ABD=BAC (2)
Từ (1) và (2)=> góc DAB-BAC=ABC-ABD
hay DAC=DBC
Mà DBC=90 độ
=> DAC=90 độ
hay AC vuông góc AD
Đúng 0
Bình luận (0)
1) Cho tam giác ABC có AB AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.a/ chứng minh PN là đường trung trực của AHb/ chứng minh tứ giác MNPH là hình thang2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB 60 độ. Gọi B , C lần lượt là hình chiếu của B, C trên AC và BD.a/ Chứng minh A, B, C 1/2 BCb/ gọi E là trung điểm BC, chứng minh tam giác EBC là tam giác đều
Đọc tiếp
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh A, B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
1) Cho tam giác ABC có AB AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.a/ chứng minh PN là đường trung trực của AHb/ chứng minh tứ giác MNPH là hình thang2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB 60 độ. Gọi B , C lần lượt là hình chiếu của B, C trên AC và BD.a/ Chứng minh B, C 1/2 BCb/ gọi E là trung điểm BC, chứng minh tam giác EBC là tam giác đều
Đọc tiếp
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
Cho hình thang cân ABCD(AB//CD), AB=BC và BC vuông góc với BD
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc hình thang
c) Gọi O là giao điểm của 2 đường chéo. Chứng minh rằng O cách đều 2 cnhj bên và đáy lớn
d) Gọi M là giao điểm cảu AD và Bc. H là hình chiếu của O trên DC. Chứng minh M,H,O thẳng hàng
1) Cho hình thang cân ABCD (AB // CD). a) Chứng minh:. b) Gọi E là giao điểm của AC và BD. Chứng minh: . 2) Cho hình thang cân ABCD có đáy nhỏ CD = a , . Đường chéo AC vuông góc với cạnh bên BC. a) Tính các góc của hình thang. b) Chứng minh AC là phân giác của góc . c) Tính diện tích của hình thang.
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.
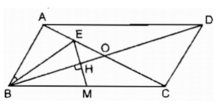
Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 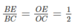
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).
Đúng 0
Bình luận (0)











