Chứng tỏ rằng hai đường thẳng vuông góc hai cạnh của 1 góc (khác góc bẹt) thì cắt nhau.

Những câu hỏi liên quan
chứng tỏ rằng hai đường thẲNG VUÔNG GÓC VỚI HAI CẠNH CỦA MỘT GÓC( KHÁC GÓC BẸT THÌ KHÁC NHAU) THÌ Cắt nhau
Câu hỏi của Uyêb Lê Minh - Toán lớp - Học toán với OnlineMath
Em tham khảo.
Đúng 0
Bình luận (0)
chứng tỏ 2 đường thẳng vuông góc với hai cạnh của 1 góc (khác góc bẹt) thì cắt nhau
cm rằng 2 đường thẳng vuông góc với 2 cạnh của 1 góc (khác góc bẹt) thì cắt nhau
Đúng 0
Bình luận (0)
giả sử góc đó là xAy và 2 đường thẳng là a ,b
ta có a vuông góc Ax và b vuông góc Ay
mà xAy không phải là góc bẹt hay Ax và Ay không thẳng hàng
nên a không song song với b
hay a cắt b
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng tỏ rằng: hai đường thẳng vuông góc với 2 cạnh của 1 góc khóc góc bẹt thì cắt nhau
chứng tỏ rằng 2 đường thẳng vuông góc với 2 cạnh của 1 góc (khác góc bẹt) thì cắt nhau
vào đây:chứng tỏ 2 đường thẳng vuông góc với hai cạnh của 1 góc (khác góc bẹt) thì cắt nhau
Đúng 0
Bình luận (0)
Chứng tỏ rằng 2 đường thẳng vuông góc với 2 cạnh của 1 góc( khác góc bẹt) thì cắt nhau
góc Ax và b vuông góc Ay
mà xAy không phải là góc bẹt hay Ax và Ay không thẳng hàng
nên a không giả sử góc đó là xAy và 2 đường thẳng là a ,b
ta có a vuông song song với b
hay a cắt b
Đúng 0
Bình luận (0)
gọi 2 đường thằng vuông góc đó là d1,d2 ... gọi d1 vuông góc cạnh a, d2 vuông góc cạnh b của góc
giả sử d1, d2 không cắt nhau => d1 song song d2
=> a song song b hoặc a trùng b, điều này trái với giả thiết a, b là 2 cạnh của 1 góc khác góc bẹt
=> giả thiết sai => điều phải chứng mình là đúng
Đúng 0
Bình luận (0)
Cho góc đỉnh O khác góc bẹt. Trên hai cạnh của góc O lấy hai điểm C và D, sao cho OC = OD. Hai đường thẳng lần lượt vuông góc với hai cạnh của góc O tại C và D cắt nhau ở E. Chứng minh rằng OE là tia phân giác của góc O.
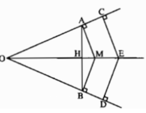
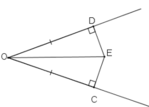
Xét ΔODE và ΔOCE vuông tại D và C có:
OE chung
OD = OC (gt)
⇒ ΔODE = ΔOCE ( cạnh huyền- cạnh góc vuông)
⇒ ∠DOE = ∠COE
⇒ OE là phân giác của góc O
Đúng 0
Bình luận (0)
cm rằng 2 đường thẳng vuông góc với 2 cạnh của 1 góc (khác góc bẹt) thì cắt nhau
Câu hỏi của Uyêb Lê Minh - Toán lớp - Học toán với OnlineMath
Em tham khảo
Đúng 0
Bình luận (0)
Cho góc đỉnh O khác góc bẹt
a) Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng AB⊥OMAB⊥OM
b) Trên hai cạnh của góc O lấy hai điểm C và D, sao cho OC = OD. Hai đường thẳng lần lượt vuông góc với hai cạnh của góc O tại C và D cắt nhau ở E. Chứng minh rằng OE là tia phân giác của góc O.
Giải
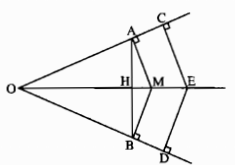
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
Đúng 0
Bình luận (0)
Cho góc đỉnh O khác góc bẹt
a) Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng \(AB\perp OM\)
b) Trên hai cạnh của góc O lấy hai điểm C và D, sao cho OC = OD. Hai đường thẳng lần lượt vuông góc với hai cạnh của góc O tại C và D cắt nhau ở E. Chứng minh OE là tia phân giác của góc O.
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.
Đúng 0
Bình luận (0)




















