CMR: an+4 - an ⋮ 30 với mọi n là số nguyên dương
Các bạn làm giúp mình nhé
Những câu hỏi liên quan
Cho a1 = 14 , a2 = 144 , an = 144...4(n chữ số 4 ) . Tìm tất cả các số nguyên dương n sap cho an là số chính phương .
GIÚP MÌNH VỚI !
Cho a,b là các số dương thỏa mãn a^2+b^2=1.
CMR a^2018+b^2018<1
Mọi người giúp mình với. Các bạn nhớ ghi cách làm ra nhé. ai nhanh mình tick cho nha
Cho dãy số
(
a
n
)
thỏa mãn
5
a
n
+
1
-
a
n
3
3
n
+
2
với mọi n
≥...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn 5 a n + 1 - a n = 3 3 n + 2 với mọi n ≥ 1. Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Chọn A
Với số tự nhiên n ≥ 1, ta có:
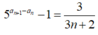
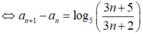
Suy ra:
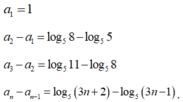
Cộng tương ứng hai vế các đẳng thức trên ta có 
với mọi số tự nhiên n
≥
1
Để 
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
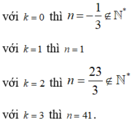
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
Đúng 0
Bình luận (0)
CMR: Với mọi số nguyên a,b,c ta luôn tìm được số nguyên dương sao cho số \(f\left(n\right)=n^3+an^2+bn+c\) không phải là số chính phương.
Giả sử f(n) là số chính phương với mọi n nguyên dương
Đặt \(f\left(n\right)=n^3+On^2+Ln+M\)
Suy ra \(f\left(1\right)=1+O+L+M\);\(f\left(2\right)=8+4O+2L+M\);\(f\left(3\right)=27+9O+3L+M\);\(f\left(4\right)=64+16O+4L+O\) đều là số chính phương.
Mà \(f\left(4\right)-f\left(2\right)\equiv2L\left(mod4\right)\) và\(f\left(4\right)-f\left(2\right)\equiv0,1,-1\left(mod4\right)\)(do \(f\left(4\right),f\left(2\right)\)đều là số chính phương)
Do đó= \(2L\equiv0\left(mod4\right)\)
Suy ra \(2L+2\equiv2\left(mod4\right)\)
Mặt khác \(f\left(3\right)-f\left(1\right)\equiv2L+2\left(mod4\right)\)
=>Mâu thuẫn với điều giả sử (do \(f\left(3\right)-f\left(1\right)\equiv0,1,-1\left(mod4\right)\))
=>Đpcm
Vậy luôn tồn tại n nguyên dương sao cho \(f\left(n\right)=n^3+On^2+Ln+M\)không phải là số chính phương.
Đúng 1
Bình luận (0)
cmr : với mọi a,b,c thuộc Z luôn tìm được số nguyên dương n thỏa mãn f(n)=n3+an2+bn+c không là số chính phương
cmr : với mọi a,b,c thuộc Z luôn tìm được số nguyên dương n thỏa mãn f(n)=n3+an2+bn+c không là số chính phương
cmr : với mọi a,b,c thuộc Z luôn tìm được số nguyên dương n thỏa mãn f(n)=n3+an2+bn+c không là số chính phương
cmr : với mọi a,b,c thuộc Z luôn tìm được số nguyên dương n thỏa mãn f(n)=n3+an2+bn+c không là số chính phương
cmr : với mọi a,b,c thuộc Z luôn tìm được số nguyên dương n thỏa mãn f(n)=n3+an2+bn+c không là số chính phương
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
3
3
n
+
2...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên
A. n = 41
B. n = 39
C. n = 49
D. n = 123
