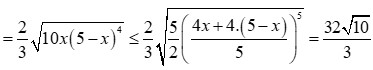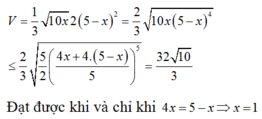cho một hình vuông cạnh 1cm người ta cắt ở mỗi góc một tam giác vuông cân để được bắt giặt đều .tính tổng dien tichcác tam giac bi cat di

Những câu hỏi liên quan
cho một hình vuông cạnh 1cm người ta cắt ở mỗi góc một tam giác vuông cân để được bắt giặt đều. Tính tổng diện tích của 4 tam giác vuông cân bị cắt đi. Giúp mình với ạ. Mk đag cần gấp ạ.
Xem chi tiết
Đặt độ dài cạnh bát giác đều là \(a\left(cm\right),0< a< 1\)
Độ dài cạnh góc vuông của tam giác vuông bị cắt đi là: \(\frac{1-a}{2}\)(cm).
Độ dài cạnh huyền của tam giác vuông đó là: \(\frac{1-a}{2}.\sqrt{2}=\frac{1-a}{\sqrt{2}}\left(cm\right)\)
đó cũng chính là độ dài cạnh của bát giác đều.
Ta có: \(a=\frac{1-a}{\sqrt{2}}\)
\(\Leftrightarrow a=\sqrt{2}-1\)(thỏa mãn)
Độ dài cạnh góc vuông của tam giác vuông là:
\(\frac{1-\left(\sqrt{2}-1\right)}{2}=\frac{2-\sqrt{2}}{2}\)(cm)
Tổng diện tích của bốn tam giác vuông bị cắt đi là:
\(\frac{1}{2}\left(\frac{2-\sqrt{2}}{2}\right)^2.4=3-2\sqrt{2}\left(cm^2\right)\)
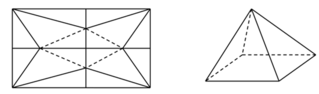
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x4 B. x2 C. x1 D. x3
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
A. x=4
B. x=2
C. x=1
D. x=3
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x 4 B. x 2 C. x 1 D.
x
3
4
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
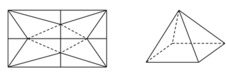
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
Đáp án là C
Hình chóp tạo thành có đáy là hình vuông diện tích
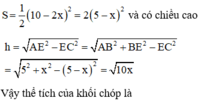

Đúng 0
Bình luận (0)
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x 4 B. x 2 C. x 1 D.
x
3
4
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm, người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
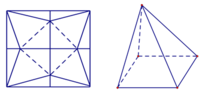
Một tấm nhôm hình vuông cạnh 10cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất. A. x 4 B. x 2 C. x 1 D.
x
3
4
Đọc tiếp
Một tấm nhôm hình vuông cạnh 10cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn tam giác cân bằng nhau (xem hình vẽ), mỗi tam giác cân có chiều cao bằng x, rồi gấp tấm nhôm đó dọc theo đường nét đứt để được một hình chóp tứ giác đều. Tìm x để khối chóp nhận được có thể tích lớn nhất.
A. x = 4
B. x = 2
C. x = 1
D. x = 3 4
Chọn đáp án C
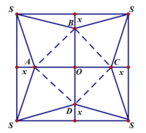
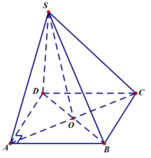
Đặt tên các điểm như hình vẽ
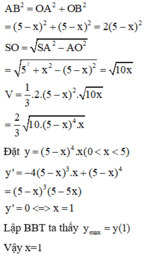
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia Cb cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt BC tại L. Chứng minh rằng:
a) Tam giac DIL là một tam giác cân;
b) tổng 1/DI2 +1/DK2 không đổi khi I thay đổi trên cạnh AB.
a) Xét hai tam giác IAD và LCD có:
+DA=DC
+ Góc IAD=Góc LCD=90 (độ)
+ Góc ADI=Góc LDC (cùng phụ với góc IDC)
Hai tam giác đó bằng nhau, nên DI=DL (tam giác IDL câ tại D)
b) Theo câu a) ta có DI=DL
nên: 1/DI.DI+1/DK.DK=1/DL.DL+1/DK.DK
DL và DK là hai cạnh góc vuông của tam giác vuông KDL, đường cao DC, áp dụng hệ thức lượng trong tam giác vuông (nghịch đảo bình phương đường cao, bằng tổng nghịch đảo hai cạnh góc vuông)
ta có: 1/DL.DL+1/DK.DK=1/DC.DC=1/a.a (a: cạnh hình vuông, không đổi)
tick đúng cho mih nhé
Đúng 1
Bình luận (0)
Đây là đề bài của e chị ạ, chị làm giúp em nha:
Cho hình vuông ABCD và điểm I ko thay đổi giữa A và B.Tia DI cắt BC tại E, đường thẳng qua D vuông góc với DE cắt BC tại F.
a; Chứng minh tam giác DIF vuông cân
Đúng 0
Bình luận (0)
cho em hỏi nếu giải theo lớp 8 thì làm kiểu gì ?Cô giáo em cũng cho bài này
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổng
1
DI
2
+
1
DK
2
không đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
1 DI 2 + 1 DK 2
không đổi khi I thay đổi trên cạnh AB.
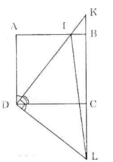
a) Xét hai tam giác vuông ADI và CDL có:
AD = CD (cạnh hình vuông)
![]()
Nên ΔADI = ΔCDL (cạnh góc cuông và góc nhọn)
Suy ra DI = DL hay ΔDIL cân. (đpcm)
b) Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
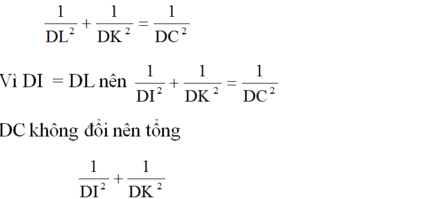
không đổi khi I thay đổi trên cạnh AB. (đpcm)
Đúng 0
Bình luận (0)
Tam giác ABC vuoing góc ở A có tổng số đo hai cạnh góc vuông bằng 7cm, cạnh AB hơn cạnh AC 1cm. Cạnh BC lớn hơn cạnh AC 2cm
a) hãy tính diện tích của một hình vuông có chu vi bằng chu vi tam giác vuông ABC
b) diện tích hình vuông ấy gấp diện tích tam giác vuông ABC bao nhiêu lần
mn giup mik vs ak, mik can gap, mik camon ak
Đúng 0
Bình luận (0)
ai nhanh nhat miktick choa ak, giup mik vs dc ko ak vi mik can gap
Đúng 0
Bình luận (0)
Cho 4 tam giác vuông có 2 cạnh góc vuông của mỗi tam giác vuông đều là 3cm và 4cm. Người ta ghép 4 tam giác vuông đó thành 1 hình vuông ABCD (như hình vẽ). Tính cạnh của hình vuông ABCD.






 '
'