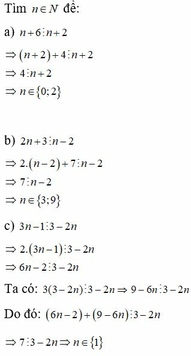a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2

=> 4 ⋮ n+2

=> n ∈ {0;2}

b, 2n+3 ⋮ n - 2

=> 2.(n - 2)+7 ⋮ n - 2

=> 7 ⋮ n - 2

=> n ∈ {3;9}

c, 3n - 1 ⋮ 3 - 2n

=> 2.(3n - 1) ⋮ 3 - 2n

=> 6n - 2 ⋮ 3 - 2n

Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n

Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n

=> 7 ⋮ 3 - 2n => n ∈ {1}

a) => n-1+3 chia hết n-1

Mà n-1 chia hết n-1

=> 3 chia hết cho n-1

=> n-1 thuộc Ước của 3

........

b)=> 2(n+1) +5 chia hết n+1

mà 2(n+1) chia hết n+1

=> 5 chia hết cho n+1

=> n+1 thuộc ước của 5

.......

a,Ta có :\(n+2⋮n-1\)

\(=>n-1+3⋮n-1\)

Do \(n-1⋮n-1\)

\(=>3⋮n-1\)

\(=>n-1\inƯ\left(3\right)\)

\(=>n-1\in\left\{-3;-1;1;3\right\}\)

\(=>n\in\left\{-2;0;2;4\right\}\)

b,\(2n+7⋮n+1\)

\(=>2.\left(n+1\right)+5⋮n+1\)

Do \(2.\left(n+1\right)⋮n+1\)

\(=>5⋮n+1\)

\(=>n+1\inƯ\left(5\right)\)

\(=>n+1\in\left\{-5;-1;1;5\right\}\)

\(=>n\in\left\{-6;-2;0;4\right\}\)

a, n + 2 ⋮ n - 1

=> n - 1 + 3 ⋮ n - 1

=> 3 ⋮ n - 1

=> n - 1 thuộc Ư(3)

=> n - 1 thuộc {-1;1-3;3}

=> n thuộc {0;2;-2;4}

b, 2n + 7 ⋮ n + 1

=> 2n + 2 + 5 ⋮ n + 1

=> 2(n + 1) + 5 ⋮ n + 1

=> 5  ⋮ n + 1

=> n + 1 thuộc Ư(5)

=> n + 1 thuộc {-1; 1; -5; 5}

=> n thuộc {-2; 0; -6; 4}

c, 2n + 1 ⋮ 6 - n

=> 2n + 1 ⋮ n - 6

=> 2n - 12 + 13 ⋮ n - 6

=> 2(n - 6) + 13 ⋮ n  -6

=>  13 ⋮ n - 6

=> n - 6 thuộc Ư(13)

Ta có: \(n^2+1=\left(n-1\right)^2+2n\)

Để \(n^2+1\)chia hết cho n-1 thì 2n phải chia hết cho n-1

Ta có 2n=2(n-1)+2

Mà n thuộc N => n-1 thuộc N

=> n-1 thuộc Ư (2)={1;2}

Nếu n-1=1 => n=2

Nếu n-1=2 => n=3

a. n² + 1 ⋮ n - 1

=> n² - 1 + 2 ⋮ n - 1

=> (n - 1)(n + 1) + 2 ⋮ n - 1

=> 2 ⋮ n - 1

b, n² + 2n + 6 ⋮ n + 4 

=> n² + 8n + 16 - 6n - 10 ⋮ n + 4

=> (n + 4)² - (6n + 10) ⋮n + 4

=> 6n + 10 ⋮ n + 4

=> 6n + 24 - 14 ⋮ n + 4

=> 6(n + 4) - 14 ⋮ n + 4

=> 14 ⋮ n + 4

b) Đầu tiên lấy n^2+2n+6 chi hết cho n+4 ta được thương là n-2 dư 14

    Để n^2-2n+6 chia hết cho n+4 hay n+4 thuooch Ư(14)

   Mà n thuộc n nên n+4 thuộc N

   Nên ta có : n+4=1=> n+-3( loại)

                     n+4=2=> n=-2 (loại)

                     n+4=7=>n=3 (thỏa mãn)

                     n+4=14=>n=10 ( thỏa mãn)

Vậy để phép chia trên là phép chia hết thì n=3 hoặc n=10

              Chúc bạn học tốt ^^

\(b,n+4⋮n+2\)

\(\Rightarrow n+2+2⋮n+2\)

       \(n+2⋮n+2\)

\(\Rightarrow2⋮n+2\)

\(\Rightarrow n+2\inƯ\left(2\right)=\left\{1;2\right\}\)

\(\Rightarrow n\in\left\{-1;0\right\}\) mà n thuộc N

=> n = 0

d, \(2n+6⋮n+3\)

\(\Rightarrow2\left(n+3\right)⋮n+3\)

        \(n+3⋮n+3\Rightarrow2\left(n+3\right)⋮n+3\)

\(\Rightarrow\) n = bao nhiêu cx đc miễn là n thuộc N

a)n={-3;-1;-5;0}

b)n={-3;-1;-5;0}

c)n=rỗng

d)n=rỗng

2n + 1 ⋮ 6 - n

=> 2n + 1 ⋮ n - 6

=> 2n - 12 + 13 ⋮ n - 6

=> 2(n - 6) + 13 ⋮ n - 6

=> 13 ⋮ n - 6

=> n - 6 thuộc Ư(13)

=> n - 6 thuộc {-1; 1; - 13; 13}

=> n  thuộc {5; 7; -7; 19}

\(2n+1⋮6-n\)

\(\Rightarrow2\left(6-n\right)+12+1⋮6-n\)

\(\Rightarrow2\left(6-n\right)+13⋮6-n\)

\(\Rightarrow13⋮6-n\)

\(\Rightarrow6-n\inƯ\left(13\right)=\left\{1;13\right\}\)

\(\text{Khi 6-n=1}\)\(\Rightarrow n=5\left(\text{Nhận}\right)\)

\(\text{Khi 6-n=13}\)\(\Rightarrow n=-7\left(\text{Loại}\right)\)

Để A thuộc luôn tồn tại mà n thuộc Z suy ra n+8 chia hết cho 2n-5

   suy ra (n+8).2 chia hết cho n+8 hay2n+16

Suy ra (2n+16)-(2n-5) chian hết cho 2n-5

suy ra 21 chia hết cho 2n-5suy ra 2n-5 thuộc Ư(21)={-21;;21;3;-3;7;-7;1;-1}

                                                 suy ra 2n thuộc{-16;26;8;2;12;-2;6;4}

                                                suy ra n thuộc{-8;13;4;1;6;-1;3;2}

Vậy n thuộc{-8;13;4;1;6;-1;3;2}