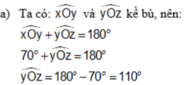cho góc xoy và góc yoz là hai góc kề bù tính xoy biết yoz=1/5 xoy

Những câu hỏi liên quan
Cho góc xOy và góc yOz là hai góc kề bù. Biết góc xOy chia 5 bằng góc yOz chia 4. Tính góc xOy, góc yOz
Cho góc xOy và góc yOz là hai góc kề bù,biết góc yOz=2.góc xOy
Tính góc xOy và góc yoz
Ta có : \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
Mà \(\widehat{yOz}=2\widehat{xOy}\)
=> \(\widehat{xOy}+2\widehat{xOy}=180^0\)
=> \(3\widehat{xOy}=180^0\)
=> \(\widehat{xOy}=60^0\)
Theo đề bài có \(\widehat{yOz}=2\widehat{xOy}\Leftrightarrow\widehat{yOz}=2\cdot60^0=120^0\)
Vậy : ...
Vì \(\widehat{xOy}\)và \(\widehat{yOz}\)là 2 góc kề bù \(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^o\)
mà \(\widehat{yOz}=2.\widehat{xOy}\)
\(\Rightarrow\widehat{xOy}+2.\widehat{xOy}=180^o\)\(\Rightarrow3.\widehat{xOy}=180^o\)\(\Rightarrow\widehat{xOy}=60^o\)
\(\Rightarrow\widehat{yOz}=180^o-60^o=120^o\)
Vậy \(\widehat{xOy}=60^o\)và \(\widehat{yOz}=120^o\)
Bài giải
Hai góc xOy và yOz là hai góc kề bù =>xOy+yOz =180 (độ)
xOy+xOy.2=180( độ)
3.xOy =180(độ)
xOy =180:3(độ)
xOy =60(độ)
Ta có: yOz=2.xOy =>yOz=60.2=120(độ)
Cho góc xOy và góc yOz là hai góc kề bù. Biết yOz 4xOy . 1) Tính: xOy và yOz . 2) Gọi Om là tia phân giác của yOz . Tính xOm.
tính góc xOy,yOz biết hai góc là góc kề bù va 1 phần 4 góc xOy bằng 1 phần 5 góc yoz
Cho 2 góc xOy và yOz là 2 góc kề bù . Biết yOz = 5 xOy
a , tính góc xOy và yOz
b, Gọi Om là tia phân giác của yOz . Tính góc xOm
Giải
a) +) Tính \(\widehat{xOy}\)
Theo đề bài, ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\) (kề bù)
hay \(\widehat{xOy}+5\widehat{xOy}=180^0\)
\(\Leftrightarrow6\widehat{xOy}=180^0\)
\(\Leftrightarrow\widehat{xOy}=180^0\div6\)
\(\Leftrightarrow\widehat{xOy}=30^0\)
+) Tính \(\widehat{yOz}\)
Theo đề bài, ta có: \(\widehat{yOz}=5\widehat{xOy}\)
hay \(\widehat{yOz}=5.30^0\)
\(\Leftrightarrow\widehat{yOz}=150^0\)
b) Vì Om là tia phân giác của \(\widehat{yOz}\) nên \(\widehat{yOm}=\widehat{mOz}=\frac{\widehat{yOz}}{2}=\frac{150^0}{2}=75^0\)
Vì Om nằm giữa Oz và Oz mà \(\widehat{xOy}\) và \(\widehat{yOz}\) kề bù nên Oy nằm giữa Ox và Om.
\(\Rightarrow\widehat{xOy}+\widehat{yOm}=\widehat{xOm}\)
hay \(30^0+75^0=\widehat{xOm}\)
\(\Leftrightarrow\widehat{xOm}=105^0\)
Vậy \(\widehat{xOm}=105^0\)
Đúng 0
Bình luận (0)
vẽ hai góc kề bù xoy và yoz biết xoy 80 tính yoz cho ot là tia phân giác của góc yoz ot là tia phân giác của góc xoy chứng tỏ tot là góc vuông
Cho hai góc kề bù xOy và yOz. Biết ∠xOy= 70 0
a) Tính số đo góc yOz
1. Cho hai góc kề bù xOy và yOz, biết góc xOy 400 a. Tính số đo góc yOz. b. Vẽ tia Ot là tia phân giác của góc yOz. Tính số đo góc yOt, góc xOt. 2. Trên cùng nửa mặt phẳng có bờ chứa tia Ox. Vẽ hai tia Oy, Oz sao cho góc xOz 400 , góc xOy 1100 . a. Tính số đo góc yOz. b. Vẽ tia Ot là tia đối của tia Ox. Chứng minh tia Oy là tia phân giác của góc tOz. ...
Đọc tiếp
1. Cho hai góc kề bù xOy và yOz, biết góc xOy = 400 a. Tính số đo góc yOz. b. Vẽ tia Ot là tia phân giác của góc yOz. Tính số đo góc yOt, góc xOt. 2. Trên cùng nửa mặt phẳng có bờ chứa tia Ox. Vẽ hai tia Oy, Oz sao cho góc xOz = 400 , góc xOy = 1100 . a. Tính số đo góc yOz. b. Vẽ tia Ot là tia đối của tia Ox. Chứng minh tia Oy là tia phân giác của góc tOz. 3. Cho hai tia Oy, Oz cùng nằm trên nủa mặt phẳng có bờ chứa tia Ox. Biết góc xOy = 300 , góc xOz = 1200 . a. Tính số đo góc yOz. Góc yOz là góc gì ? b. Vẽ tia phân giác Om của góc xOz. Tính số đo góc zOm, góc yOm. 4. Vẽ góc vuông xOy. Vẽ tia Oz sao cho Oz, Oy cùng nằm trên nửa mặt phẳng có bờ chứa tia Ox. Biết góc xOz = 300 . a. Tính số đo góc yOz. b. Vẽ Ot là tia phân giác của góc xOz. Tính số đo góc yOt. 5. Cho góc xOy = 1200 . Vẽ Oz là tia đối của tia Ox. Vẽ tia Ot trên cùng nửa mặt phẳng bờ chứa tia Ox sao cho góc zOt = 1300 . a. Tính số đo góc yOz. b. Chứng minh tia Oy nằm giữa hai tia Oz, Ot ? c. Tính số đo góc xOt.
Xem thêm câu trả lời
Cho hai góc kề bù xoy và yoz kề bù biết xoy-yoz=40
Tính số đo của xoy và yoz . vẽ hình minh họa
vì xoy và yoz là 2 góc kề bù =>xoz=180o
mà xoy-yoz=40o (dạng toán tổng hiệu)
xoy= (xoz+40o):2=(180+40):2=110o
yoz=180-110=70o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời