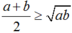Cho các số dương a, b, c, dsao cho b bằng trung bình cộng của a; c và \(\frac{1}{c}=\frac{1}{2}\left[\frac{1}{b}+\frac{1}{d}\right]\)
Chứng minh 4 số a, b, c, d lập thành một tỉ lệ thức
Cho a b c d là các số thực dương có tổng bằng một cmr a bình trên a cộng b cộng với b bình trên b cộng c cộng với c bình trên c cộng d cộng với d bình trên d cộng a lớn hơn bằng 1/2
Bài 1. Trung bình cộng của ba số A,B,C là 1460, trung bình cộng của số A và C là 1520. Tìm số B Bài 2. Trung bình cộng của ba số A,B,C là 896, trung bình cộng của số A và C là 860, trung bình cộng của A và B là 920. Tìm A, B, C Bài 3. Trung bình cộng của 5 số là 1672 trung bình cộng của 4 số sau là 1860. Tìm số đầu. các bạn giải nhanh giúp mình mình sắp phải nộp cho cô rồi
Bài 2:
Tổng của A, B, C là:
\(896\times3=2688\)
Tổng của A và C là:
\(860\times2=1720\)
Tổng của A và B là:
\(920\times2=1840\)
Số B là:
\(2688-1720=968\)
Số C là:
\(2688-1840=848\)
Số A là:
\(2688-968-848=872\)
Bài 3:
Tổng của 5 số là:
\(1672\times5=8360\)
Tổng của 4 số sau là:
\(1860\times4=7440\)
Số đầu là:
\(8360-7440=920\)
Bài 1:
Tổng của A, B, C là:
\(1460\times3=4380\)
Tổng của A và C là:
\(1520\times2=3040\)
Số B là:
\(4380-3040=1340\)
Trung bình cộng của ba số tự nhiên A, B và C là 72. Biết rằng số A bằng trung bình cộng của số B và C; số B bằng 4/5 số C. Tìm các số A, B?
A bằng TBC của B và C nên A = 1/2 tổng của B và C
Chia tổng của B và C Thành 2 phần băng nhau thì A là 1 phần như thế
Tổng số phần bằng nhau là
1+2=3 phần
Giá trị 1 phần hay giá trị của A là
72:3=24
Tổng của B và C là
72-24=48
Chia số B thành 4 phần bằng nhau thì số C là 5 phần
Tổng số phần bằng nhau là
4+5=9 phần
Giá trị 1 phần là
48:9 lẻ => xem lại đề bài
Cho 4 số nguyên dương a;b;c;d trong đó b bằng trung bình cộng của a và c ;1/c=1/2*(1/b+1/d)Chứng minh rằng 4 số trên lập thành 1 tỉ lệ thức
Cho a,b,c là các số dương. CMR nếu b là trung bình cộng của a và c thì \(\frac{1}{\sqrt{a}+\sqrt{b}}+\frac{1}{\sqrt{b}+\sqrt{c}}=\frac{2}{\sqrt{c}+\sqrt{a}}\)
program so_lon_nhat;
uses crt;
var a: array[1..100] of integer;
i,n,max,k,dem: integer;
s,tbc: real;
begin
clrscr;
writeln(' nhap so phan tu cua day'); readln(n);
for i:=1 to n do
begin
writeln('a[',i,']'); readln(a[i]);
end;
writeln(' nhap so can tim:'); readln(k);
max:=a[1];
i:=1;
dem:=0;
for i:=1 to n do
begin
if max<a[i] then max:=a[i];
s:=s+a[i];
tbc:=s/n;
if a[i]=k then dem:=dem+1;
end;
writeln(' so lon nhat trong day tren la:',max);
while (i<n) and (a[i]<>k) do i:=i+1;
if a[i]=k then writeln(' phan tu thu ', i ,' bang ',k)
else writeln(' k tim dc phan tu',k);
writeln(tbc:6);
writeln('co', dem, ' phan tu', k);
readln
end.
Cho n số nguyên dương( ko nhất thiết khác nhau) trong đó có số 68. Trung bình cộng của n số đó bằng 56. Khi bỏ số 68 thì trung bình cộng của n-1 số còn lai bằng 55
a/Tìm n
b/ Số lớn nhất trong n số đã cho có thể bằng bao nhiêu?
a. Ta có:
(Tổng các số n)/n = 56
Theo đề bài, ta có phương trình:
\(\frac{56n-68}{n-1}=55\)
<=> 56n - 68 = 55(n-1)
<=> 56 - 55n = 68 - 55
<=> n = 13
b. Tổng của 13 số nguyên dương đã cho: 56 x 13 = 728
Tổng của 12 số nguyên dương còn lại khi bỏ 68: 728 - 68 = 660
Mà số nguyên dương bé nhất là 1
=> Tổng của 11 số nguyên dương bé nhất (ko nhất thiết phải khác nhau) là 11.
Số nguyên dương lớn nhất cần tìm là: 660 - 11 = 649
Để tính trung bình cộng của 3 số a,b,c bạn tâm lấy trung bình cộng của a và b, rồi lấy trung bình cộng của kết quả này với c. Cho biết a>b>c. Chứng minh rằng cách tính của tâm cho kết quả nhỏ hơn kết quả đúng.
Các bác giúp em với!
Nếu lấy trung bình cộng 3 số a, b,c thì ta được kết quả: \(\frac{a+b+c}{3}\)
Nếu lấy trung bình cộng của a và b, rồi lấy trung bình cộng của kết quả này với c, ta được kết quả: \(\frac{\frac{a+b}{2}+{c}}{2}\)
Ta xét biểu thức \(\frac{a+b+c}{3}-\frac{\frac{a+b}{2}+{c}}{2}=\frac{a+b+c}{3} - \frac{a+b+2c}{4}=\frac{4a+4b+4c-3a-3b-6c}{12}=\frac{a+b-2c}{12}\)
Đến đây, vì \(a>b>c \Rightarrow a+b>2c \iff a+b-2c>0 \iff \frac{a+b-2c}{12}>0\)
Từ đây ta có thể suy ra \(\frac{a+b+c}{3}>\frac{\frac{a+b}{2}+c}{2} \Rightarrow đpcm\)
Sử dụng bất đẳng thức để viết các mệnh đề sau
a) x là số dương.
b) y là số không âm.
c) Với mọi số thực α, |α| là số không âm.
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng.
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0,