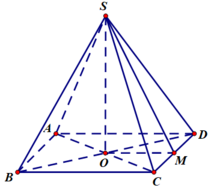
Cho hình vuông ABCD có cạnh bằng a, M là trung điểm của BC. Tính giá trị đúng của cos AMD.

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).
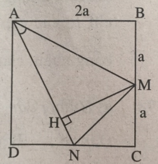
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
Đúng 1
Bình luận (0)
Cho Hình vuông ABCD cạnh a. M là trung điểm của AB . Tính giá trị biểu thức : (AB +AD)(BD+BC)
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính \(\cos\widehat{MAN}\) ?
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau:
(
A
B
→
+
A
D
→
)
.
(
B
D
→
+
B
C
→
)
A. a2 B. –a2 C. 2a2 D. Đáp á...
Đọc tiếp
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau: ( A B → + A D → ) . ( B D → + B C → )
A. a2
B. –a2
C. 2a2
D. Đáp án khác
Chọn A.
Theo quy tắc hình bình hành ta có ![]()
Do đó
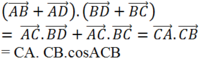
(![]() vì AC và BD vuông góc với nhau)
vì AC và BD vuông góc với nhau)
Mặt khác ![]() và theo định lý Pitago ta có:
và theo định lý Pitago ta có:
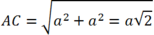
Suy ra ![]()
![]()
Đúng 0
Bình luận (0)
cho hình vuông ABCD . biết M và N theo thứ tự là trung điểm của BC và CD biết tam giác AMD cân tại M . tính COS góc MAN
Cho hình chóp S. ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông. Gọi M là trung điểm của CD. Giá trị
M
S
→
.
C
B
→
bằng A.
a
2
2
B.
-
a
2
2
C. ...
Đọc tiếp
Cho hình chóp S. ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông. Gọi M là trung điểm của CD. Giá trị M S → . C B → bằng
A. a 2 2
B. - a 2 2
C. a 2 3
D. 2 a 2 2
cho hình thang abcd có s 120cm2 biết đáy ab = 2/3 cd . m là trung điểm của cạnh bc . nối a với m , d với m. tính s abm , amd
GIẢI RÕ ĐÚNG MK TICK VN NÓI LÀ LÀM
Nối A với C;B với D.
Ta có:S ABC = 2/3 S ADC (vì AB=2/3 DC;chiều cao là chiều cao hình thang ABCD.)
=> S ABC=2/5 S ABCD
S ABM=1/2 S ABC( vì BM=1/2 BC;chung chiều cao hạ từ A xuống BM và BC)
S ABM = 1/2 S ABC
S ABM = 1/2(2/5 S ABCD)
S ABM = 1/5 S ABCD = 120:5=24(cm2)
Ta lại có:S BCD=3/2 S ABD(CD=3/2 AB;chiều cao là chiều cao hình thang ABCD) =>S BCD=3/5 S ABCD
S MDC=1/2 S BCD(MC=1/2 BC;chung chiều cao hạ từ đỉnh D xuống MC và BC)
S MDC=1/2 S BCD=1/2(3/5 S ABCD)=3/10 S ABCD=120:10x3=36(cm2)
S AMD=S ABCD -S MDC-S ABM=120-36-24=60(cm2)
Đ/s:AMD=60cm2;ABM=24 cm2
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh là 10, M là trung điểm của BC.
a) Tính giá trị của | vectơ AB+ vectơ AD| và vectơ DM. vectơ DA
b)Tìm tập hợp điểm P thỏa mãn vectơ PA.vectơ BC=10
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết MN
a
6
2
. Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng A.
2
5
. B.
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết MN = a 6 2 . Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng
A. 2 5 .
B. 3 3 .
C. 5 5 .
D. 3 .
Chọn B
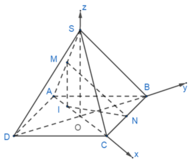
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
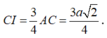
Xét tam giác CNI có
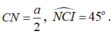
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
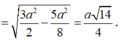
Mà MI//SO
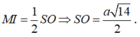
Chọn hệ trục tọa độ như hình vẽ. Ta có:
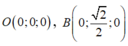
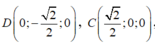
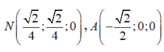
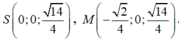
Khi đó
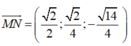
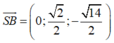
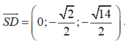
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
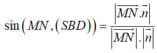
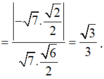
Đúng 0
Bình luận (0)