Dùng tính chất giao hoán để tìm kết quả của phép tính 6 x 15.
Những câu hỏi liên quan
Hãy thực hiện các phép tính sau : a,
x
y
:
y
z
b,
y
z
:
x
y
c,
x
y
:
y
z
:
z
x
d,
x
y
:...
Đọc tiếp
Hãy thực hiện các phép tính sau :
a, x y : y z
b, y z : x y
c, x y : y z : z x
d, x y : y z : z x
So sánh kết quả của a với kết quả của b; kết quả của c với kết quả của d
Phép chia có tính chất giao hoán và tính chất kết hợp hay không ?
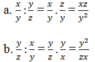
Kết quả câu b là nghịch đảo kết quả câu a.
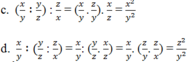
Kết quả câu c và d khác nhau. Phép chia không có tính chất giao hoán, tính chất kết hợp.
Đúng 0
Bình luận (0)
Căn cứ vào tính chất giao hoán và kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số. Ví dụ. Tính chất giao hóa của phép nhân phân số: Bằng cách tương tự em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
Đọc tiếp
Căn cứ vào tính chất giao hoán và kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Ví dụ. Tính chất giao hóa của phép nhân phân số:
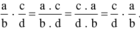
Bằng cách tương tự em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta có:
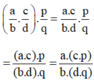
(áp dụng tính chất kết hợp của số nguyên cho cả tử và mẫu)
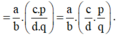
Vậy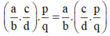 
(tính chất kết hợp của phép nhân phân số)
Đúng 0
Bình luận (0)
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân phân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp cua phép nhân phân số.Ví dụ: Tính chất giao hoán của phép nhân phân số :frac{a}{b}.frac{c}{d}frac{c.a}{d.b}frac{c}{d}.frac{a}{b}.Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
Đọc tiếp
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân phân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp cua phép nhân phân số.
Ví dụ: Tính chất giao hoán của phép nhân phân số :
\(\frac{a}{b}.\frac{c}{d}=\frac{c.a}{d.b}=\frac{c}{d}.\frac{a}{b}\).
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q
ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)
Theo tính chất kết hợp của phép nhân các số nguyên ta có:
(a.c).p = a.(c.p) và b. (d.q) = (b. d) . q.
Do đó: (ab.cd).pq=ab.(cd.pq)
Đúng 0
Bình luận (0)
Cho ví dụ về tính chất giao hoán và tính chất kết hợp của phép cộng các số tự nhiên.
Cho ví dụ về tính chất giao hoán và kết hợp của phép nhân các số tự nhiên.
VD: - Tính chất giao hoán của phép cộng: 1 + 2 = 2 +1
- Tính chất kết hợp của phép cộng: 1 + 2 + 8 = 1 + (2+8)
- Tính chất giao hoán của phép nhân: 1.2 = 2.1
- Tính chất kết hợp của phép nhâ: 2.45.50 = (2.50).45
Đúng 0
Bình luận (0)
Thực hiện phép cộng rồi dùng tính chất giao hoán để thử lại: 45,08 + 24,97
Thực hiện phép cộng rồi dùng tính chất giao hoán để thử lại: 9,46 + 3,8
9 , 46 + 3 , 8 13 , 26 thử lại 3 , 8 + 9 , 46 13 , 26
Đúng 0
Bình luận (0)
Thực hiện phép cộng rồi dùng tính chất giao hoán để thử lại: 45,08 + 24,97
45 , 08 + 24 , 97 70 , 05 thử lại 24 , 97 + 45 , 08 70 , 05
Đúng 0
Bình luận (0)
Thực hiện phép cộng rồi dùng tính chất giao hoán để thử lại: 0,07 + 0,09
0 , 07 + 0 , 09 0 , 16 thử lại 0 , 09 + 0 , 07 0 , 16
Đúng 0
Bình luận (0)
Thực hiện phép cộng rồi dùng tính chất giao hoán để thử lại: 9,46 + 3,8
