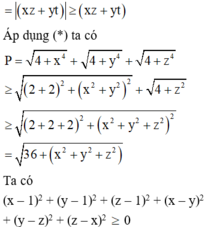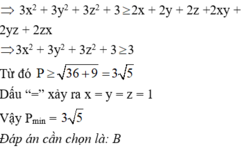Cách 1:

Ta có \(A=xy+yz+2zx\)

\(\Rightarrow A+1=x^2+y^2+z^2+xy+yz+2zx\)

                    \(=\left(x+z+\frac{y}{2}\right)^2+\frac{3}{4}y^2\ge0\)

\(\Rightarrow A\ge-1\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}y=0\\x=-z\end{cases}}\)

Ta có : \(\left(x+y+z\right)^2\ge0\)

\(\Rightarrow xy+yz+zx\ge\frac{-\left(x^2+y^2+z^2\right)}{2}=-\frac{1}{2}\)

Lại có : \(\left(x+z\right)^2\ge0\Rightarrow xz\ge\frac{-\left(x^2+z^2\right)}{2}=\frac{y^2-1}{2}\ge-\frac{1}{2}\)

Khi đó : \(xy+yz+2zx\ge-1\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}y=o\\x^2=z^2=\frac{1}{2}\end{cases}}\)

Cách 2

Ta có : \(\left(x+y+z\right)^2\ge0\)

\(\Leftrightarrow xy+yz+zx\ge\frac{-\left(x^2+y^2+z^2\right)}{2}=\frac{-1}{2}\)

Mặt khác: \(\left(x+z\right)^2\ge0\Rightarrow xz\ge\frac{-\left(x^2+z^2\right)}{2}=\frac{y^2-1}{2}\ge\frac{-1}{2}\)

\(\Rightarrow xy+yz+2xz\ge-1\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}y=0\\x=-z\end{cases}}\)

khó quá!!!!!!!!!!!

Áp dụng BĐT Cô - si cho 2 số \(\frac{xy}{z};\frac{yz}{x}\)dương ta có: \(\frac{xy}{z}+\frac{yz}{x}\ge2\sqrt{\frac{xy}{z}.\frac{yz}{x}}=2\sqrt{y^2}=2y\)(1)

Tương tự. \(\frac{yz}{x}+\frac{zx}{y}\ge2\sqrt{\frac{yz}{x}.\frac{zx}{y}}=2\sqrt{z^2}=2z\) (2);

\(\frac{xy}{z}+\frac{zx}{y}\ge2\sqrt{\frac{xy}{z}.\frac{zx}{y}}=2\sqrt{x^2}=2x\)(3)

Cộng từng vế của (1)(2)(3) ta được \(2.\left(\frac{xy}{z}+\frac{yz}{x}+\frac{zx}{y}\right)\ge2\left(x+y+z\right)=2\Rightarrow P\ge1\)

Vậy Min P = 1 tại x= y = z = 1/3

k cho minh nha

giúp mình với

bạn giải ra giúp mình với

ta có \(xy\le\left(\frac{x+y}{2}\right)^2\) và \(yz+xz=z\left(x+y\right)\le\frac{z^2+\left(x+y\right)^2}{2}\)

\(\Rightarrow5=xy+yz+xz\le\left(\frac{x+y}{2}\right)^2+\frac{z^2+\left(x+y\right)^2}{2}=\frac{3}{4}\left(x+y\right)^2+\frac{1}{2}z^2\)

Xét \(3x^2+3y^2+z^2\ge\frac{3}{2}\left(x+y\right)^2+z^2=2\left(\frac{3}{4}\left(x+y\right)^2+\frac{1}{2}z^2\right)\ge2\cdot5=10\)

dấu "=" xảy ra khi \(\hept{\begin{cases}x=y\\z=x+y\end{cases}\Leftrightarrow\hept{\begin{cases}x=y=\pm1\\z=\pm2\end{cases}}}\)