cho hình thang ABCD gọi MN là trung điểm của đáy AD,BC điểm O thuộc MN .Qua O kẻ đường thẳng song song với đáy hình thẳngcắt AD,CD tai E,F .CM OE=OF

Những câu hỏi liên quan
cho hình thang ABCD gọi M,N là trung điểm của đáy AD,BC điểm O thuộc MN .Qua O kẻ đường thẳng song song với đáy hình thẳng cắt AD,CD tai E,F .CM OE=OF
cho hình thang abcd. gọi m là trung điểm của ab, n là trung điểm của cd. lấy o bất kỳ trên mn, kẻ đường thẳng qua o // với 2 đáy ab và cd cắt ad tai e và cắt bc tại f. Chứng minh oe=of
Gọi M, N theo thứ tự là các trung điểm của hai đáy AD và BC của hình thang ABCD. Từ điểm O tùy ý thuộc đoạn MN, kẻ đường thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên tại E và F. Chứng minh rằng O là trung điểm của EF.
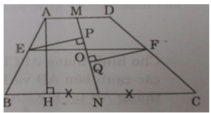
Ta có MA = MD, NC = NB (gt) và AD // BC.
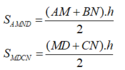
⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)
Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM
⇒ SAEM = SDFM
Tương tự SBEN = SNFC
⇒ SAMNB - (SAEM + SBEN) = SDMNC - (SBEN + SNFC)
hay SEMN = SFMN
Hai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQ
Xét ΔEPO và ΔFQO có:
∠EOP = ∠QOF (đối đỉnh)
EP = PQ (cmt)
∠EPO = ∠FQO = 90o
Do đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
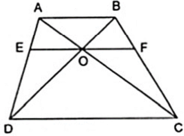
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
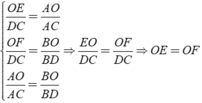
Điều phải chứng minh.
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
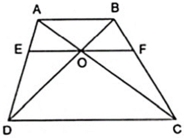
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
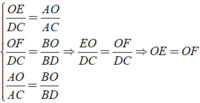
Điều phải chứng minh.
Đúng 0
Bình luận (0)
Cho hình thang ABCD có các cạnh đáy AB = a, CD = b. Gọi O là giao điểm của hai đường chéo, qua O kẻ đường thẳng song song với 2 đáy, cắt cạnh bên AD và BC tại M và N.CMR MN=2ab/a+b
Cho hình thang ABCD với AB song song CD, AB<CD. Gọi trung điểm của đường chéo BD là M. Qua M kẻ đường thẳng song song với DC cắt AC tại N. Gọi E là trung điểm của AB, O là giao điểm của AD và BC, OE cắt CD tại F. Chứng minh F là trung điểm của CD.
Cho hình thang ABCD ( AB//CD), Gọi M,N lần lượt là trung điểm của AB<CD, O là giao điểm của AC và BD; I là giao điểm của AD,BC
a) chứng minh O,I,M,N thẳng hàng
b) Qua O kẻ đường thẳng song song với AB cắt AD,BC lần lượt tại E,F. Chứng minh OE=OF
alodgdhgjkhukljhkljyutfruftyhf
Cho hình thang ABCD ( AB // CD). Gọi O là giao điểm của AC và BD. Qua O vẽ đường thẳng song song AB, CD cắt AD và BC lần lượt tại M và N
a) CM: O là trung điểm của MN
b) CM: 1/AB + 1/CD = 1/CM
c) CM: S tam giác OAD = S tam giác OBC
d) Gọi E là giao điểm của AD và BC. Gọi F là giao điểm của OE và CD. CM: F là trung điểm của CD










