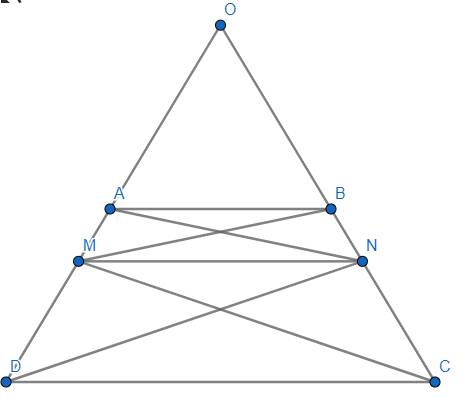
trên cạnh AB của hình chữ nhật ABCD lấy điểm M và N sao cho AM = BN ( M nằm giữa A và N ) Chứng minh MNCD là hình thang cân

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có chiều dài 10cm, chiều rộng 5cm. Trên cạnh AB lấy hai điểm M và N sao cho MN = 1 phần 2 AB. Tìm tỉ số diện tích của hình thang MNCD và hình chữ nhật ABCD?
các bạn giúp mình với, nhớ làm bài giải nhé.
giúp mình đi, mình k cho
Đúng 0
Bình luận (0)
Diện tích hình chữ nhật ABCD là S(ABCD) = AB.BC;
Diện tích hình thang MNCD là S(MNCD) = 1/2.(MN + CD).BC = 1/2.(1/2.AB + AB).BC = 1/2.3/2.AB.BC = 3/4.AB.BC = 3/4.S(ABCD)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình chữ nhật ABCD có AB= 42cm, AD= 30cm trên AB lấy điểm M và điểm N sao cho AM=1/4 của AB, AN=NB. Tính diện tích hình thang MNCD
8.Cho hình chữ nhật ABCD có diện tích là 2700cm2.
Trên AD lấy điểm M sao cho AM AD, AD 45 cm,
Trên BC lấy N sao cho BN BC....
Đọc tiếp
8.Cho hình chữ nhật ABCD có diện tích là 2700cm2.
Trên AD lấy điểm M sao cho AM= AD, AD= 45 cm,
Trên BC lấy N sao cho BN = BC.
a. Các cạnh song song với MN là . …………………………
b. Các cạnh vuông góc với DC là .……………………………...............................................
c. Tính diện tích hình chữ nhật MNCD và ABNM
……………………………………………………………………………………………………………………
cho hình vuông ABCD vuông tại A lấy hai điểm M và N theo thứ tự thuộc cạnh AB và BC sao cho AM = CN.O là tâm của hình vuông,MO cắt DC tại E . Lấy F đống xứng E qua BD
a) chứng minh AMNC là hình thang cân
b) chứng minh MBED là hình bình hành
c) chứng minh MNEF là hình chữ nhật
d) tìm vị trí của điểm M trên để tứ giác MNEF là hình vuông
cho hình thang cân abcd/ lấy m thuộc ad, n thuộc bc sao cho am=bn. cm tứ giác abnm , mncd là hình thang cân. tìm vị trí của m, n lần lượt trên ad, bc sao cho mn = (ab+dc): 2. Hãy CM điều đó
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).
Đúng 2
Bình luận (0)
Bài 1:Cho hình thang cân ABCD (Ab song song với CD)có ABAd và BDDC.Tính các góc của hình thang này.Bài 2:Cho tam giác ABC đều.Vẽ đường vuông góc với BC tại C cắt AB tại E.Vẽ đường vuông góc với AB tại A cắt BC tại F.Chứng minh rằng ACFE là hình thang cân.Bài 3:Cho tam giác ABC cân tại A ,M là điểm bất kì nằm giữa A và B.Trên tia đối của CA lấy điểm N sao cho CNBM.Vẽ ME và NF lần lượt vuông góc với đường thẳng BC.Gọi I là giao điểm của MN và BC.a)Chứng minh : IEIFb)Trên cạnh AC lấy điểm D sao cho...
Đọc tiếp
Bài 1:Cho hình thang cân ABCD (Ab song song với CD)có AB=Ad và BD=DC.Tính các góc của hình thang này.
Bài 2:Cho tam giác ABC đều.Vẽ đường vuông góc với BC tại C cắt AB tại E.Vẽ đường vuông góc với AB tại A cắt BC tại F.Chứng minh rằng ACFE là hình thang cân.
Bài 3:Cho tam giác ABC cân tại A ,M là điểm bất kì nằm giữa A và B.Trên tia đối của CA lấy điểm N sao cho CN=BM.Vẽ ME và NF lần lượt vuông góc với đường thẳng BC.Gọi I là giao điểm của MN và BC.
a)Chứng minh : IE=IF
b)Trên cạnh AC lấy điểm D sao cho CD=CN.Chứng minh rằng BMDC là hình thang cân.
Bài 4:Cho tam giác ABC cân ở A ;M là trung điểm của BC.Trên tia AM lấy điểm N;BN cắt AC ở D,CN cắt AB ở E.Chứng minh BEDC là hình thang cân
Bài 5:Cho hình thang cân ABCD (AB song song với CD) ; góc D=60 độ,AD=AB
a)Chứng minh :DB là phân giác góc ADC
b)Chứng minh : DB vuông góc với BC
Cho hình chữ nhật ABCD có chiều dài 10cm,chiều rộng 5cm.Trên cạnh AB lấy hai điểm M và N sao cho MN=1phần2 AB.Tìm tỉ số diện tích của hình thang MNCD và hình chữ nhật ABCD ?
cho hình chữ nhật ABCD có chiều dài 10cm và chiều rộng 5cm.Trên cạnh AB lấy 2 điểm M và N sao cho MN bằng 1/2 AB.Tìm tỉ số diện tích của hình thang MNCD và hình chữ nhật ABCD.
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD . Lấy điểmP trên cạnh BD ( P nằm giữa O và D ). Gọi M là điểm đối xứng với C qua P .a) Chứng minh AMDB là hình thang. Xác định vị trí điểm P trên BD để AMBDlà hình thang cân.b) Kẻ ME AD MF AB , . Chứng minh rằng EF AC // và E F P , , thẳng hàng.c) Trên cạnh AB lấy điểm X , trên DC lấy điểm J sao cho AX CJ lấy N làđiểm tùy ý trên AD . Gọi G là giao điểm của XJ và NB , H là giao điểm của XJ vàNC . Tính diện tích của tứ giác AXJ...
Đọc tiếp
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD . Lấy điểm
P trên cạnh BD ( P nằm giữa O và D ). Gọi M là điểm đối xứng với C qua P .
a) Chứng minh AMDB là hình thang. Xác định vị trí điểm P trên BD để AMBD
là hình thang cân.
b) Kẻ ME AD MF AB , . Chứng minh rằng EF AC // và E F P , , thẳng hàng.
c) Trên cạnh AB lấy điểm X , trên DC lấy điểm J sao cho AX CJ lấy N là
điểm tùy ý trên AD . Gọi G là giao điểm của XJ và NB , H là giao điểm của XJ và
NC . Tính diện tích của tứ giác AXJD theo S S ABCD . Chứng minh rằng
S S S AXGN NHJD GBCH