cho tam giác ABC có góc B, góc C là góc nhọn, AC>AB. Kẻ đường cao AH. CMR: góc HAB<góc HAC
Những câu hỏi liên quan
Cho tam giác ABC có ∠B , ∠C là các góc nhọn, AC > AB. Kẻ đường cao AH. Chứng minh rằng ∠(HAB) < ∠(HAC) .
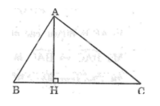
Trong ΔABC ta có AC > AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B và góc C là các góc nhọn, AC > AB. Kẻ đường cao AH.
Chứng minh rằng :
\(\widehat{HAB}< \widehat{HAC}\)
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (AB<AC) có đường cao AH. Tù H kẻ HM vuông góc vớ AB tại M, N vuông góc với AC tại N.
a) CMR ta giác HAB đồng dạng với tam giác MAH
CMR tam giác HAC đồng dạng với tam giác NAH
b) CM AM.AB=AH^2 và AM.AB=AN.AC
c) CM tam giác AMN đồng dạng với tamm giác ACB.
d) Gọi I là giao điểm của AH và MN. CM IA.MH=IM.AN
e) Gọi K là giao điểm của BC. CM AK vuông góc với IN.
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.
a. CMR: góc HAB = góc MAC.
b. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. CMR: AM vuông góc với DE.
a)Xét tam giác HAB vuông tại A=>góc HAB=90o - B(1)
Xét tam giác vuông ABC có trung tuyến AM ứng với cạnh huyền BC
=>MA=1/2BC=>MA=MC
=>tam giác CMA cân tại M
=>góc MCD=góc MAC
mà góc MCA=90o-B(Xét tam giác vuông ABC)
=>góc MAC=90o-B(2)
Từ (1) và (2) ta có góc HAB=góc MAC
Đúng 1
Bình luận (0)
Cho tam giác tam giác ABC có 3 góc nhọn kẻ AH vuông góc BC(H thuộc BC).Biết HB<HC. CMR: góc HAB<góc HAC
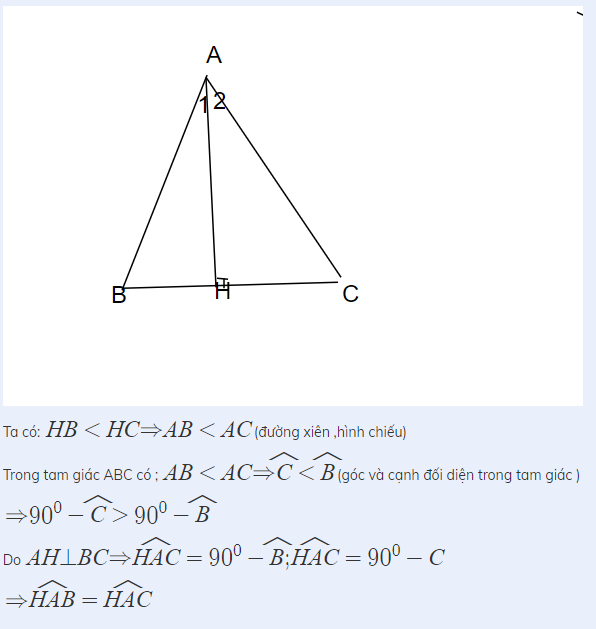
tham khảo tại: https://olm.vn/hoi-dap/detail/215686516317.html
Đúng 2
Bình luận (0)
cho tam giác ABC có AB<AC kẻ AH vuông góc với BC tại H. CM HB<HC góc HAB<góc HAC xét 2 trường hợp góc B là góc tù và góc nhọn
Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ AH vuông góc với BC tại H. So sánh H A B ^ và H A C ^ .
CÂU TRẢ LỜI CHÍNH XÁC NÈ
Cho tam giác nhọn ABC kẻ đường cao AH từ H kẻ HE vuông góc với AB kẻ HF vuông góc với AC
a, cmr AE.AB=AF.AC
b,AB =5cm AH=7 cm tính AE, BE
c, cho góc HAC =30° tính FC
Cho tam giác nhọn ABC kẻ đường cao AH từ H kẻ HE vuông góc với AB kẻ HF vuông góc với AC
a, cmr AE.AB=AF.AC
b,AB =5cm AH=7 cm tính AE, BE
c, cho góc HAC =30° tính FC