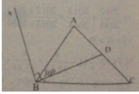
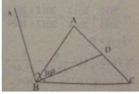
1.cho tam giác ABC có góc ABC=55 độ.Trên cạnh AC lấy điểm D sao cho góc ABD =30 độ.
a,tính góc DBC
b, từ B kẻ Bx sao cho góc DBx=90 độ.Tính góc ABx
2.một người đi hết quảng đường AB trong 3 giờ.Giờ thứ nhất đi được 40 km,giờ thứ 2 đi 9/10 quảng đường giờ thứ nhất đi,và bằng 4/5 quảng đường giờ thứ ba đi.Tính quảng đường AB
MONG CÁC BẠN GIẢI GIÚP HAI BÀI TOÁN NÀY!
CHIỀU NAY MÌNH NỘP RỒI!
BẠN NÀO GIÚP ĐƯỢC THÌ MÌNH TÍCH CHO!