Những câu hỏi liên quan
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD AB. Lấy G thuộc cạnh AC sao cho
A
G
1
3
A
C
. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.Chứng minh:a) G là trọng tâm tam giác BCD;b)
∆
B
E
D
∆...
Đọc tiếp
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho A G = 1 3 A C . Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.
Chứng minh:
a) G là trọng tâm tam giác BCD;
b) ∆ B E D = ∆ F D E , từ đó suy ra EC = DF;
c) ∆ D M F = ∆ C M E ;
d) B, G, M thẳng hàng.
cho tam giác ABC có góc B = 90 độ(BA>BC) trên tia đối tia BC lấy điểm D sao cho BC = BD
a,cm tam giác ABC = tam giác ABD và AC=AD
b,qua D kẻ đường thẳng song song với đường thẳng AC cắt AB ở E cm AC = DE
c,qua E kẻ đường thẳng vuông góc với đường thẳng AC cắt đường thẳng BC ở K cm EC vuông góc AK
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho AG = AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD. Chứng minh: a) G là trọng tâm tam giác BCD. b) , từ đó suy ra EC = DF
Cho tam giác ABC cân tại A, các đường thẳng qua B vuông góc với AB và qua C vuông góc với AC cắt nhau tại Sa) Chứng minh tam giác SBC cânb) Trên tia đối của tia BS lấy điểm D, trên tia đối của tia CS lấy điểm E sao cho CEBD. Chứng minh rằng DE song song BCBài 3: Cho tam giác ABC. Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân ở A là ABD và ACE. Dựng AH vuông góc với BC, đường thẳng HA cắt DE ở K. Dựng AI vuông góc với DE, đường thẳng IA cắt BC tại M. Chứng minh rằng:a) Tam giác AEK Tam gi...
Đọc tiếp
Cho tam giác ABC cân tại A, các đường thẳng qua B vuông góc với AB và qua C vuông góc với AC cắt nhau tại S
a) Chứng minh tam giác SBC cân
b) Trên tia đối của tia BS lấy điểm D, trên tia đối của tia CS lấy điểm E sao cho CE=BD. Chứng minh rằng DE song song BC
Bài 3: Cho tam giác ABC. Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân ở A là ABD và ACE. Dựng AH vuông góc với BC, đường thẳng HA cắt DE ở K. Dựng AI vuông góc với DE, đường thẳng IA cắt BC tại M. Chứng minh rằng:
a) Tam giác AEK = Tam giác CAM
b) KD = KE
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
1. Câu hỏi của 1234567890 - Toán lớp 7 - Học toán với OnlineMath
Cho tam giác ABC có M là trung điểm của BC ( AB<AC ). Trên tia đối của MA lấy D sao cho MA=MD
a, Chứng minh: AC song song với BD
b, Trên nửa mặt phẳng bờ AD ko chúa điểm B vẽ tia Ax song song với BD. Trên tia Ax lấy E sao cho AE=BC.
Chưng minh :ba điểm E, C, D thẳng hàng
c, Qua M kẻ đường thẳng song song với AC cắt CD tại F
ChứNG Minh: EF= 1/2 AC
Cho tam giác ABC có M là trung điểm của BC ( AB<AC ). Trên tia đối của MA lấy D sao cho MA=MD
a, Chứng minh: AC song song với BD
b, Trên nửa mặt phẳng bờ AD ko chúa điểm B vẽ tia Ax song song với BD. Trên tia Ax lấy E sao cho AE=BC.
Chưng minh :ba điểm E, C, D thẳng hàng
c, Qua M kẻ đường thẳng song song với AC cắt CD tại F
ChứNG Minh: EF= 1/2 AC
Cho tam giác ABC vuông tại A có AB AC. Gọi M là trung điểm của cạnh BC, D là trung điểm của cạnh ACa). Chứng minh rằng: ∆AMB ∆AMC và AM ⊥ BCb) Từ A kẻ đường thẳng vuông góc với BD, cắt BC tại E. Trên tia đối của tia DE lấy điểm F sao cho DF DE. Chứng minh rằng: ∆ADF ∆CDE, từ đó suy ra: AF // CEc) Từ C dựng đường thẳng vuông góc với AC, cắt AE tại G. Chứng minh rằng ∆BAD ∆ACGd) Chứng minh rằng: AB 2CG
Đọc tiếp
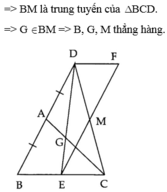
Cho tam giác ABC vuông tại A có AB = AC. Gọi M là trung điểm của cạnh BC, D là trung điểm của cạnh AC
a). Chứng minh rằng: ∆AMB = ∆AMC và AM ⊥ BC
b) Từ A kẻ đường thẳng vuông góc với BD, cắt BC tại E. Trên tia đối của tia DE lấy điểm F sao cho DF = DE. Chứng minh rằng: ∆ADF = ∆CDE, từ đó suy ra: AF // CE
c) Từ C dựng đường thẳng vuông góc với AC, cắt AE tại G. Chứng minh rằng ∆BAD = ∆ACG
d) Chứng minh rằng: AB = 2CG
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔADF và ΔCDE có
DA=DC
\(\widehat{ADF}=\widehat{CDE}\)
DF=DE
Do đó: ΔADF=ΔCDE
Xét tứ giác AECF có
D là trung điểm của AC
D là trung điểm của FE
Do dó: AECF là hình bình hành
Suy ra: AF//EC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên tia đối của AB, lấy D sao cho ABAD, lấy G thuộc AC sao cho AGfrac{1}{3}AC, E là giao điểm của DE và BC. Qua E, vẽ đường thẳng song song với BD. Qua D, vẽ đường thẳng song song với BC. 2 đường thẳng này cắt nhau tại F. Chứng minh:a)G là trọng tâm tam giác BCDb)Tam giác BED tam giác FDE, ECDFc)Tam giác DMF tam giác CMEd)B,G,M thẳng hàng
Đọc tiếp
Cho tam giác ABC. Trên tia đối của AB, lấy D sao cho AB=AD, lấy G thuộc AC sao cho AG=\(\frac{1}{3}\)AC, E là giao điểm của DE và BC. Qua E, vẽ đường thẳng song song với BD. Qua D, vẽ đường thẳng song song với BC. 2 đường thẳng này cắt nhau tại F. Chứng minh:
a)G là trọng tâm tam giác BCD
b)Tam giác BED= tam giác FDE, EC=DF
c)Tam giác DMF= tam giác CME
d)B,G,M thẳng hàng
tham khảo nha:https://h.vn/hoi-dap/question/785855.html