Tam Giác ABC Vuông Tại A Phân Giác BD Cắt AH Tại E.
a) chừng minh tam giác ADE Cân
b) chứng minh AE.AD=BE.BC
c) kẻ DK vuông góc với BC tại K Tứ giác ADKE là hình gì?
Cho tam giác ABC vuông tại A, đường cao AH, phân giác BD cắt AH tại E. a) Chứng minh tam giác ADE cân; b) Chứng minh AE BD BE DC . . ; = c) Từ D kẻ DK BC ⊥ tại K. Tứ giác ADKE là hình gì?
Cho tam giác ABC vuông tại A (AB< AC) AH là đường cao, Tia phân giác của góc CAH cắt BC tại D Qua D kẻ DK vuông góc AC tại K . Tia phân giác của góc ABC cắt DK tại E.
a)Chứng minh tam giác BAD cân
b)Chứng minh tứ giác ABDE là hình thoi.
c)Tìm điều kiện của tam giác vuông ABC để tứ giác ABCE là hình thang cân.
Cho tam gíac ABC vuông tại A, đường cao AH, phân giác BD cắt AH tại E.
a) Chứng minh tam giác ADE cân
b) Chứng minh AE.BD=BE.DC
c) Từ D kẻ DK vuông góc BC tại K. Tứ giác ADEK là hình gì?
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAC
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAK
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
b ) Xét tam giác ABD và tam giác KBD , có
BD cạnh chung
góc ABD = góc KBD ( gt )
BA = BK ( tam giác ABK cân tại B )
suy ra tam giác ABD = tam giác KBD ( c.g.c)
suy ra góc BAD = góc BKD ( 2 góc tương ứng)
mà góc BAD = 90 độ
suy ra BKD = 90 độ
nên DK vuông góc BC
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAC
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
a) Tam giác ABK có BE vừa là đường cao vừa là phân giác nên tam giác ABK cân tại B
=> BE là đường trung trực của đoạn thẳng AK.
hay A và K đối xứng nhau qua BD.
b) Xét tam giác ABD và KBD có
AB=KB(tam giác ABK cân tại B)
Góc ABD=KBD(gt)
BD cạnh chung .
Vậy tam giác ABD và KBD bằng nhau theo trường hợp (c.g.c).
=> Góc DKB=DAB=90 độ(hai góc tương ứng)
hay DK vuông góc với BC.
c)Ta có: góc: HAK+HKA=90 độ ( cùng phụ với góc H trong tam giác AHK).
và góc: KAC+BAK= góc A= 90 độ
mà góc BAK= HKA( tam giác ABK cân tại B).
từ 3 điều này suy ra góc HAK=KAC hay AK là tia phân giác góc HAC.
d) Tam giác ABK có AH, BE là các đường cao giao nhau tại I nên I là trực tâm.
=> KI cũng là đường cao
Hay KI vuông góc với AB.
mà AC vuông góc với AB( do tam giác ABC vuông tại A)
TỪ hai điều này suy ra IK//AC
Tứ giác IKCA có IK//AC nên IKCA là hình thang.
Tam giác ABC vuông tại A.Phân giác của góc ABC cắt AC tại D.Kẻ AE vuông góc BD(E thuộc BD),AE cắt BC tại K
a Chứng minh tam giác ABK cân và K đối xứng A qua BD
b Chứng minh DK vuông góc BC
c Kẻ AH vuông góc BC(H thuộc BC).Chứng minh AK phân giác góc HAK
d AH cắt BD tại I.Chứng minh tứ giác IKCA là hình thang
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :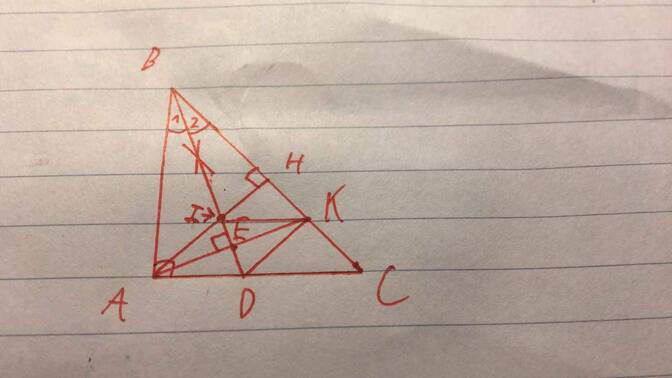
Cho tam giác ABC vuông tại A, kẻ phân giác BD của góc b (D thuộc AC). Từ A kẻ AH vuông góc BD (H thuộc BD), tia AH cắt BC tại E.
A) Chứng minh : Tam giác BHA=tam giác BHE
B) Chứng minh : ED vuông góc BC
C) Kẻ AK vuông góc BC ( K thộc BC). Chứng minh : AE là tia phân giác của góc CAK
các bạn hãy giúp mình làm nha !
a) Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)(BH là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBHA=ΔBHE(cạnh góc vuông-góc nhọn kề)
b) Ta có: ΔBHA=ΔBHE(cmt)
nên BA=BE(hai cạnh tương ứng)
Xét ΔBAD và ΔBED có
BA=BE(cmt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔBAD=ΔBED(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)