cho hình vẽ biết AM=3cm, MB=5cm. Góc CMB= 60 độ. Tính độ dài cạnh AC
Cho hình vẽ biết : AM= 3cm; MB = 5cm. Góc CMB = 60°. Tính độ dài cạnh AC
phải có cả hình thì mới biết hình gì mà tính chứ bạn nhỉ ?
C6: Cho ∆ABC, kẻ AH⊥BC. Biết AB=5cm; BH=3cm; BC=10cm. a) Biết góc C=30°. Tính góc HAC. b) Tính độ dài các cạnh AH, AC, HC Mng vẽ hình luôn nha 🤩
a. Ta có: ∠HAC + ∠AHC + ∠C = 180 ( ĐL tổng 3 góc tam giác )
∠HAC + 90 + 30 = 180
∠HAC = 180 - ( 30 + 90 )
∠HAC = 180 - 120 = 60
b. -Ta có: BC = HC + HB
10 = HC + 3
⇒ HC = 10 - 3 = 7 ( cm )
-ΔAHB ⊥ tại H ( đường cao AH )
⇒ AB² = AH² + BH² ( ĐL Py-ta-go )
5² = AH² + 3²
25 = AH² + 9
⇒AH² = 25 - 9 = 16
⇒AH = √16 = 4 ( cm )
-ΔAHC ⊥ tại H ( đường cao AH )
⇒ AC² = AH² + CH² ( ĐL Py-ta-go )
AC² = 4² + 7²
AC² = 16 + 49 = 65
⇒AC = √65 ( cm )
cho hình vẽ biết rằng: AB=AD=DC=3cm, AC=5cm, BD=2cm. tính tổng độ dài của các cạnh đó
Tổng độ dài của các cạnh đó là:
3 + 3 + 3 + 5 + 2 = 16 ( cm )
Đáp số: 16 cm.
Cho hình vẽ sau: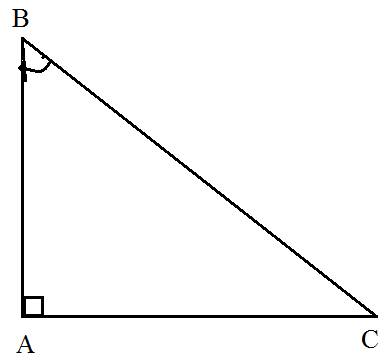
a)Biết AC = 6cm; góc B = 60 độ. Tính BC.
b)Biết AB = 5cm; góc B = 65 độ. Tính BC.
c)Biết AC = 6cm, góc B = 60 độ. Tính AB.
a) \(BC=\dfrac{AC}{sinB}=\dfrac{6}{sin60}=4\sqrt{3}\left(cm\right)\)
b) \(BC=\dfrac{AB}{cosB}=\dfrac{5}{cos65}\approx11,831\left(cm\right)\)
c) \(AB=\dfrac{AC}{tanB}=\dfrac{6}{tan60}=2\sqrt{3}\left(cm\right)\)
a) Vẽ tam giác ABC , biết góc A = 60 độ , AB = 2cm , AC = 4cm.
b) Gọi D là một cạnh thuộc điểm AC sao cho CD =3cm. Tìm độ dài đoạn AD
c) Cho biết góc ABD = 30 độ. Tính góc CBD
Cho hình thoi ABCD có diện tích là 216cm2 và chu vi là 60cm. Đoạn thẳng MN chia hình thoi thành 2 hình bình hành AMND và MBCN (như hình vẽ), biết độ dài cạnh MB hơn độ dài cạnh AM là 5cm. Tính:
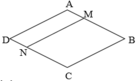
a) Chu vi hình bình hành MBCN.
b) Diện tích hình bình hành AMND.
Cạnh hình thoi ABCD là : 60 : 4 = 15 cm => tổng độ dài AM và MB là AB = 15 cm
Hiệu độ dài MB và AM là 5 cm
Độ dài cạnh MB là: (15 +5) : 2 = 10 cm
Độ dài cạnh AM là: 15 - 10 = 5 cm
a) Hình bình hành MBCN có: MB = NC = 10 cm; MN = BC = 15 cm
Chu vi hình MBCN là: MB + BC + CN + NM = 10 + 15 + 10 + 15 = 50 cm
b) Chiều cao hình thoi ABCD là: 216 : 15 = 14,4 cm
Chiều cao hình bình hành AMND bằng chiều cao hình thoi ABCD ; có đáy là AM
Diện tích hình bình hành AMND là: 14,4 x 5 = 72 cm2
Cho M và N là hai điểm lần lượt thuộc hai cạnh AB và AC của tam giác ABC.Biết MN=6cm,AM=3cm,MB=5cm,AC=16cm,NC=10cm.Tính độ dài cạnh BC ?
Ta có: \(\frac{MB}{AB}=\frac{MB}{AM+MB}=\frac{5}{8}\)
\(\frac{NC}{AC}=\frac{10}{16}=\frac{5}{8}\)
=> \(\frac{MB}{AB}=\frac{NC}{AC}\)Theo định lí Ta-lét đảo
=> MN // BC
Áp dụng hệ quả định lí Ta-lét vào \(\Delta ABC\)có MN // BC
=> \(\frac{MN}{BC}=\frac{AM}{AB}\)=> \(BC=\frac{MN.AB}{AM}=\frac{8.6}{3}=16\)
Vẽ tam giác ABC, biết độ dài các cạnh AB=3cm, AC=4cm, BC=5cm. Góc BAC bằng bao nhiêu độ
Ta có \(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\)
\(\Rightarrow AB^2+AC^2=BC^2\)Áp dụng pi- ta - go đảo ta có :
\(\Delta ABC\)vuông tại A
\(\Rightarrow\widehat{BAC}=90^o\)
NHẬN XÉT \(AB^2+AC^2=3^2+4^2=25=5^2=BC^2\)
Nên áp dụng định lý Pytago đảo ta có tam giác ABC vuông tại A
Vậy góc BAC bằng \(90^o\)
Ta thấy:AB^2+AC^2=3^2+4^2=9+16=25
BC^2=5^2=25
=>AB^2+AC^2=BC^2(=25)
=>Tam giác ABC vuông tại A(theo định lý Pi ta go đảo)
=>Góc BAC=90 độ
Vậy góc BAC=90 độ