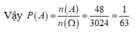Một số tự nhiên N được gọi là hào hiệp nếu nó chia hết cho tất cả các chữ số của nó và chia hết cho tổng các chữ số của nó. Ví dụ, 12 là một số hào hiệp, còn 102 thì không. Hãy tìm số hào hiệp nhỏ nhất chia hết cho 11.
ai giúp đi, 26/3 thi rồi !!!!
Những câu hỏi liên quan
Một số tự nhiên N được gọi là hào hiệp nếu nó chia hết cho tất cả các chữ số của nó và chia hết cho tổng các chữ số của nó. Ví dụ, 12 là một số hào hiệp, còn 102 thì không. Hãy tìm số hào hiệp nhỏ nhất chia hết cho 11
Tôi đoán mò ra 132 nhưng làm thế nao ra đc nó giúp tớ nhé cam on cac ban
Đúng 0
Bình luận (0)
Giải
Vì 11 ko phải là số hào hiệp nên khi số hào hiệp cần tìm chia cho 11 sẽ được một số hào hiệp nhỏ nhất có thể.
Ta có các số hào hiệp nhỏ nhất là
12:thì số hào hiệp can tìm là: 11*12=132
Đáp số : 132
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Một số tự nhiên N được gọi là hào hiệp nếu nó chia hết cho tất cả các chữ số của nó và chia hết cho tổng các chữ số của nó. Ví dụ, 12 là một số hào hiệp, còn 102 thì không. Hãy tìm số hào hiệp nhỏ nhất chia hết cho 17.
p/s: đây là câu hỏi trong MYTS năm ngoái nhé
Giải
Vì 17 không phải là một số hào hiệp nên khi số hào hiệp cần tìm chia cho 17 sẽ được một số hào hiệp mới.
Để số hào hiệp cần tìm là nhỏ nhất thì khi số hào hiệp cần tìm đó chia cho 17 sẽ được một số hào hiệp mới nhỏ nhất thỏa mãn.
Ta có các số hào hiệp nhỏ nhất là:
12.Vậy số hào hiệp cần tìm là:204(loại vì ko chia được cho 0)
24.Vậy số hào hiệp cần tìm là:408(loại vì ko chia được cho 0)
36.Vậy số hào hiệp cần tìm là:612(chọn).
Vậy số cần tìm là 612.
Đáp số:612.
Đúng 1
Bình luận (0)
Một số tự nhiên N được gọi là hào hiệp nếu nó chia hết cho tất cả các chữ số của nó và chia hết cho tổng các chữ số của nó. Ví dụ, 12 là một số hào hiệp, còn 102 thì không. Hãy tìm số hào hiệp nhỏ nhất chia hết cho 17.
p/s: đây là câu hỏi trong MYTS năm ngoái nhé
1 tháng 1 2023 lúc 9:58
số hào hiệp là một số chia hết cho tất cả các chữ số của nó và cũng chia hết cho tổng các chữ số . Ví dụ : 12 là số hào hiệp vì 12 chia hết cho 1 cho 2 cho 3 . 102 thì ko được vì ko có số nào chia hết cho 0 . Tìm số hào hiệp nhỏ nhất chia hết cho 17.
số nguyên dương k được gọi là số may mắn nếu k chia hết cho tổng các chữ số của nó . Ví dụ 12 có tổng các chữ số là 3 và 12 chia hết cho 3 nên 12 là số may mắn.số 11 có tổng các chữ số là 2 và 11 không chia hết cho 2 nên 11 không phải là số may mắn.Viết chương trình cho phép nhập số nguyên dương n từ bàn phím rồi thực hiện.a/ cho biết có bao nhiêu số may mắn nhỏ hơn nb/ in ra các số nhỏ nhất lớn hơn n và là số may mắn(Mọi người làm bằng pascal giúp mình)
Đọc tiếp
số nguyên dương k được gọi là số may mắn nếu k chia hết cho tổng các chữ số của nó . Ví dụ 12 có tổng các chữ số là 3 và 12 chia hết cho 3 nên 12 là số may mắn.số 11 có tổng các chữ số là 2 và 11 không chia hết cho 2 nên 11 không phải là số may mắn.
Viết chương trình cho phép nhập số nguyên dương n từ bàn phím rồi thực hiện.
a/ cho biết có bao nhiêu số may mắn nhỏ hơn n
b/ in ra các số nhỏ nhất lớn hơn n và là số may mắn
(Mọi người làm bằng pascal giúp mình)
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
A
.
P
1
63
B
.
P
1
126
C...
Đọc tiếp
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
A . P = 1 63
B . P = 1 126
C . P = 2 63
D . P = 8 21
Chọn A
Giả sử số cần lập là 
Số phần từ không gian mẫu: 
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
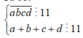
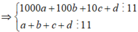
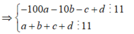
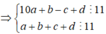
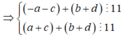
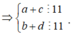
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: 
Đúng 1
Bình luận (0)
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
A . P = 1 63
B . P = 1 126
C . P = 2 63
D . P = 8 21
Xem chi tiết
1. tìm số tự nhiên n có hai chữ số, biết rằng 2n+1 và 3n+1 đều là các số chính phương.2.tìm số tự nhiên có hai chữ số, biết rằng nếu nhân nó với 45 thì được một số chính phương.3.a) Các số tự nhiên n và 2n có tổng các các chữ số bằng nhau. Chứng minh rằng n chia hết cho 9. b)* tìm số chính phương n cá ba chữ số, biết rằng n chia hết cho 5 và nếu nhân n với 2 thì tổng các chữ số của nó không đổi.
Đọc tiếp
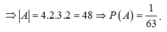
1. tìm số tự nhiên n có hai chữ số, biết rằng 2n+1 và 3n+1 đều là các số chính phương.
2.tìm số tự nhiên có hai chữ số, biết rằng nếu nhân nó với 45 thì được một số chính phương.
3.a) Các số tự nhiên n và 2n có tổng các các chữ số bằng nhau. Chứng minh rằng n chia hết cho 9.
b)* tìm số chính phương n cá ba chữ số, biết rằng n chia hết cho 5 và nếu nhân n với 2 thì tổng các chữ số của nó không đổi.
3.a)n và 2n có tổng các chữ số bằng nhau => hiệu của chúng chia hết cho 9
mà 2n-n=n=>n chia hết cho 9 => đpcm
Đúng 0
Bình luận (0)
Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
A
.
1
63
B
.
8
21
C
.
1
84
D
.
...
Đọc tiếp
Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
A . 1 63
B . 8 21
C . 1 84
D . 1 42
Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng 
Theo bài ra ta có: 
và 
Suy ra 
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là 
Chọn 2 cặp trong 4 cặp số trên để tạo số 
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48
Đúng 0
Bình luận (0)