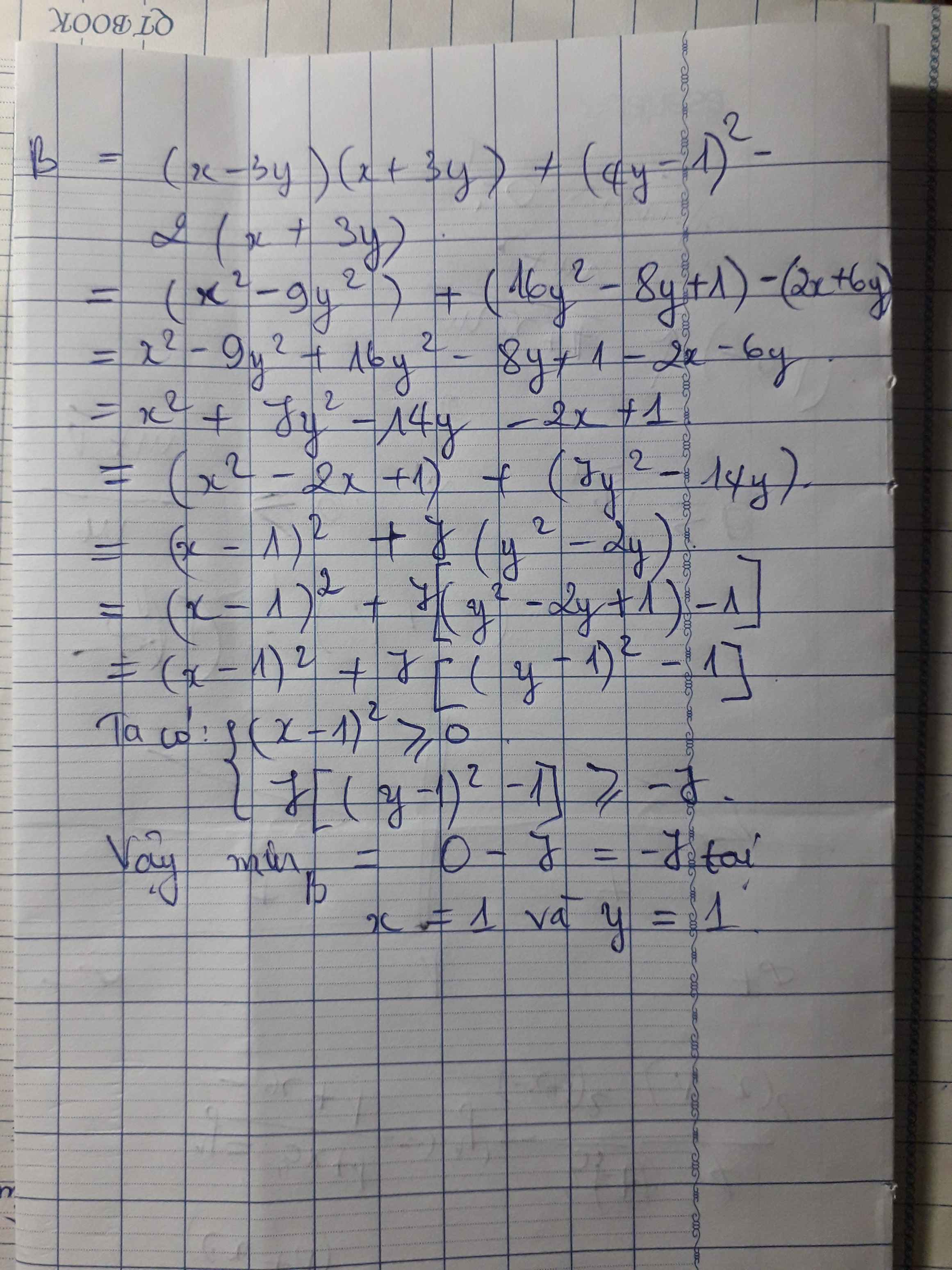cho 2x + 3y = 5
tìm giá trị nhỏ nhất của B = x^2 + 9y^2 + 2011

Những câu hỏi liên quan
Cho x,y,z là 3 số thực dương và thỏa mãn: 4x^2 + 9y^2 + 16z^2 = 1.Tìm giá trị nhỏ nhất của A = 2x / (9y^2 + 16z^2) + 3y / (4x^2 + 16 z^2) + 4z / (4x^2 + 9y^2)
a) tìm giá trị nhỏ nhất của biểu thức: A=\(x^2+xy+y^2-3x-3y+2004\)
b) TÌm giá trị nhỏ nhất của biểu thức: A=\(2x^2+9y^2-6xy-6x-12y+2006\)
c) Tìm min của y=\(\frac{x^4+x^2+5}{x^4+2x^2+1}\)
Cho B=(x-3y)(x+3y) + (4y-1)^2 - 2(x+3y) Tìm giá trị nhỏ nhất của B
Cho 2x^2+y^2 -2xy-6x+9=0 . Tính giá trị của C=3𝑥−1/2𝑦
Tìm giá trị nhỏ nhất của 2x^2+9y^2 -6xy-6x-12y+2004
Tìm giá trị lớn nhất của
a) -5-(x-1)(x+2
b) -x^2+2xy-4y^2+2x+10y-8
Cho x.0, y>0 và \(2x+3y< =2\)
Tìm giá trị nhỏ nhất của biểu thức A=\(\frac{4}{4x^2+9y^2}+\frac{9}{xy}\)
Theo cô-si thì \(2\sqrt{2x.3y}\le2x+3y\le2\Rightarrow xy\le\frac{1}{6}\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\)
\(\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{\frac{3.1}{6}}\)
\(=\frac{14}{\left(2x+3y\right)^2}+\frac{26.6}{3}=56\)
\("="\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Đúng 0
Bình luận (0)
ta thấy \(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{16}{\left(2x+3y\right)^2}+\frac{26}{3xy}\)(1)
lại có \(2x+3y\le2\Leftrightarrow\left(2x+3y\right)^2\le4\Leftrightarrow4x^2+9y^2+12xy\le4\left(2\right)\)
mặt khác \(4x^2+9y^2\ge12xy\)(theo Bất Đẳng Thức Cosi cho x,y>0) (3)
từ (1) và (2) => \(12xy+12xy\le4\Leftrightarrow3xy\le\frac{1}{2}\left(4\right)\)
từ (1) và (4) => \(A\ge\frac{16}{4}+\frac{26}{\frac{1}{2}}=4+52=56\)
dấu "=" xảy ra khi \(\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Tìm x,y sao cho
A= 2x^2 + 9y^2 - 6xy - 12y +2021 có giá trị nhỏ nhất
B= -x^2 + 2xy - 4x + 2x + 10y - 8 có giá trị lớn nhất
biết 2x + 3y = 1 tìm giá trị nhỏ nhất của biểu thức 8x^3 + 27y^3 + 4x^2 + 9y^2 + 5
\(M=8x^3+27y^3+4x^2+9y^2+5\)
\(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)+4x^2+9y^2+5\)
\(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)+4x^2+9y^2+5\)
\(=4x^2-6xy+9y^2+4x^2+9y^2+5\)
Áp dụng BĐT AM-GM có:
\(1\ge2.\sqrt{6xy}\)
\(\Leftrightarrow xy\le\frac{1}{24}\)
Dấu " = " xảy ra <=> 2x=3y <=> x=0,25 y=1/6
Áp dụng BĐT Cauchy-schwarz ta có:
\(M\ge\frac{2.\left(2x+3y\right)^2}{2}-6xy+5\ge\frac{2}{2}-\frac{6.1}{24}+5=6.25\)
Dấu " = " xảy ra <=> 2x=3y <=> x=0,25 y=1/6
KL:.....................................................................
Đúng 0
Bình luận (0)
Tìm x,y sao cho:
A= 2x^2+9y^2-6xy-6x-12y+2005 có giá trị nhỏ nhất
B= -x^2+2xy-4y^2+2x+10y-8 có giá trị lớn nhất
tìm x,y sao cho
a. A=2x^2 +9y^2-6xy-6x-12y+2014 đạt giá trị nhỏ nhất ?
b. B=-x^2 +2xy-4y^2+2x+10y-8 đạt giá trị lớn nhất ?