10^n+1.10^n.6
cac ban giup minh vs
Tính A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)
Giup minh vs cac ban oi
Chung minh: (n-3)(n+3)-(n-7)(n-3) chia het cho 10.
MInh can gap. Cac ban giup minh voi. Minh like cho.
Ta có:(n-3)(n+3)-(n-7)(n-3) (1)
=(n-3)(n+3-n+7)
=10(n-3)
Vậy PT(1) chia hết cho 10
\(\left(n-3\right)\left(n+3\right)-\left(n-7\right)\left(n-3\right)=\left(n-3\right)[n+3-\left(n-7\right)]\)
\(=\left(n-3\right)\left(n+3-n+7\right)=\left(n-3\right)\cdot10⋮10\)(ĐPCM)
cac ban oi giup minh cau nay vs
rut gon cac bieu thuc sau
3x^2 - 2x . (5+1,5x) + 10
giai giup mik vs
\(3x^2-2x.\left(5+1,5x\right)+10\)
\(=3x^2-2x.5-2x.1,5x+10\)
\(=3x^2-3x^2-10x+10\)
\(=10-10x\)
\(=10.\left(1-x\right)\)
(n+5)={-10,-5,-2,-1,1,2,5,10)
n={-15,-10,-7,-8,-4,-3,0,5}
ban nao biet thi giup minh voi nha
(10n+18.n-1):27
hãy giải thích tại sao 3^n.10-2^n.5=3^n.10-2^n-1.10
cac ban oi giup minh bai nay voi :
cho phan thuc A = \(\frac{n-5}{n+1}\)
a. tinh A khi n=10
b. tinh A khi n = 0
c. tim n de A thuoc Z
D.tim n de A la phan so toi gian
bn nao giup mk , mk cam on
a) Khi n = 10 có:
\(A=\frac{10-5}{10+1}=\frac{5}{11}\)
b) Khi n = 0
\(A=\frac{0-5}{0+1}=-\frac{5}{1}=-5\)
c) Để A thuộc Z thì n - 5 chia hết cho n + 1
=> n - 6 + 1 chia hết cho n + 1
=> n + 1 chia hết cho n + 1 => -6 chia hết n + 1
=> n + 1 thuộc Ư (6) = {1;2;3;6;-1;-2;-3;-6}
=> n thuộc {0;1;2;5;-2;-3;-4;-7}
d. Để A tối giản thì n = {0;5;-2}
Khi n = 0 ta có :
\(A=\frac{0-5}{0+1}=\frac{-5}{1}\)
A = \(\frac{n-5}{n+1}\)
a, Khi n = 10
A = \(\frac{10-5}{10+1}\) = \(\frac{5}{11}\)
b, Khi n = 0
A = \(\frac{0-5}{0+1}\) = \(-5\)
c, Tìm n để a thuộc Z
\(\Rightarrow\) n-5 \(⋮\) n+1
\(\Leftrightarrow\) n - 6+1 \(⋮\) n+1
mà n+1 \(⋮\) n+1
\(\Rightarrow\) -6 \(⋮\) n+1
\(\Rightarrow\) n + 1 \(\in\) Ư ( -6) = { -6;6;1;-1;2;3;-2;-3}
\(\Rightarrow\) n \(\in\) { 0;1;2;5;-2;-3;-4;-7}
d, tìm n để a là phân số tối giản
................................................
Chúc bạn học tốt ![]()
Giup minh bai 3 vs b4 cac ban oi minh dang can gap a pls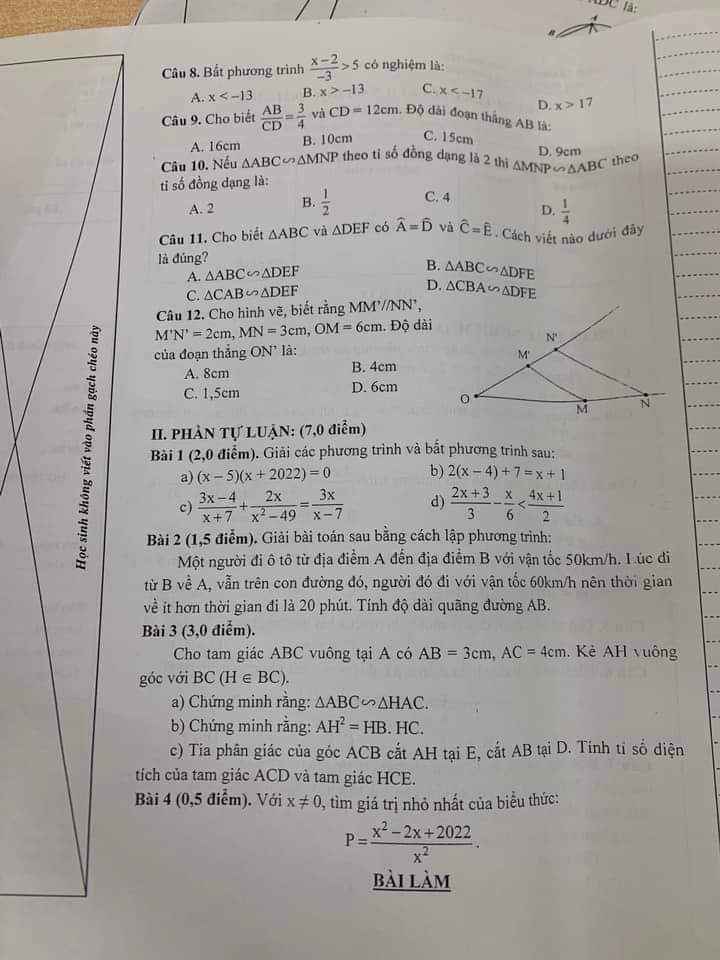
Bài 4:
\(P=\dfrac{x^2-2x+2022}{x^2}=\dfrac{2022x^2-2.2022x+2022^2}{2022x^2}=\dfrac{\left(x^2-2.2022x+2022^2\right)+2021x^2}{2022x^2}=\dfrac{\left(x-2022\right)^2}{2022x^2}+\dfrac{2021}{2022}\ge\dfrac{2021}{2022}\)\(P_{min}=\dfrac{2021}{2022}\Leftrightarrow x=2022\)
a)Cho n thuoc N. Chunng minh rang n^2 chia het cho 3 hoac n^2 chia cho 3 du 1
b) Co ton tai n thuoc N de n^2+1=30000.....000000( ko gioi han so 0)
Chung minh rang M= 10^n +18.n-1 chia het cho 27
CAC BAN GIUP MINH VOI MAI LA ,MINH NOP ROI HUUUUUUUUUUU
AI LAM XONG MINH SE TICK CHO
a,Nếu n = 3k thì n² + 1 = (3k)² + 1 = 9k² + 1 chia 3 dư 1
Nếu n = 3k + 1 thì n² + 1 = (3k + 1)² + 1 = 9k² + 6k + 2 chia 3 dư 2
Nếu n = 3k + 2 thì n² + 1 = (3k + 2)² + 1 = 9k² + 12k + 5 chia 3 dư 2
Vậy vớj mọj n thuộc Z, n^2 + 1 không chia hết cho 3
b,chọn n=1 => 10+18-1=27 chia hết cho 27 (luôn đúng)
giả sử với mọi n=k (k thuộc N*) thì ta luôn có 10^k+18k-1 chia hết cho 27.
Cần chứng minh với n=k+1 thì 10^(k+1)+18(k+1)-1 chia hết cho 27.
Ta có 10^(k+1)+18(k+1)-1= 10*10^k+18k+18-1
= (10^k+18k-1)+9*10^k+18
= (10^k+18k-1)+9(10^k+2)
ta có: (10^k+18k-1) chia hết cho 27 => 10^(k+1)+18(k+1)-1 chia hết cho 27 khi và chỉ khi 9(10^k+2) chia hết cho 27.
Chứng minh 9(10^k+2) chia hết cho 27.
chọn k=1 => 9(10+2)=108 chia hết cho 27(luôn đúng)
giả sử k=m(với m thuộc N*) ta luôn có 9(10^m+2) chia hết cho 27.
ta cần chứng minh với mọi k= m+1 ta có 9(10^(m+1)+2) chia hết cho 27.
thật vậy ta có: 9(10^(m+1)+2)= 9( 10*10^m+2)= 9( 10^m+9*10^m+2)
= 9(10^m+2) +81*10^m
ta có 9(10^m+2) chia hết cho 27 và 81*10^m chia hết cho 27 => 9(10^(m+1)+2) chia hết cho 27
=>9(10^k+2) chia hết cho 27
=>10^(k+1)+18(k+1)-1 chia hết cho 27
=>10^n+18n-1 chia hết cho 27=> đpcm
K MINH NHA!...............