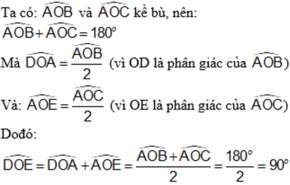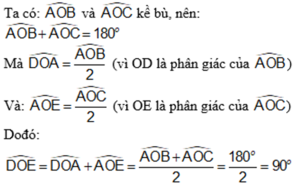cho 2 góc kề bù AOB và AOC biết góc AOB=2/7 AOC. Gọi OD là tia phân giác của góc AOC. Tính góc BOD

Những câu hỏi liên quan
Cho AOB=80 độ có . Gọi góc AOC và góc BOD là các góc kề bù với góc AOB. Chứng minh rằng:
a)Hai góc AOC và BOD là hai gócđối đỉnh.
b)Đường thẳng chứa tia phân giác của góc BOD cũng chứa tia phân giác của AOC
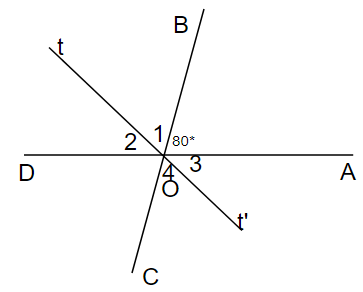
a) Vì ∠AOC kề bù với ∠AOB
⇒ OC và OB là 2 tia đối nhau và ∠AOC + ∠AOB = 1800
Vì ∠BOD và ∠AOB là 2 tia đối nhau
⇒ OA và OD là 2 tia đối nhau và ∠BOD + ∠AOB = 180o
⇒ ∠AOC = ∠BOD
Vì ∠AOC có OA là tia đối của tia OD;
∠BOD có OC là tia đối của tia OB
Mà ∠AOC = ∠BOD
⇒ ∠AOC và ∠BOD là 2 góc đối đỉnh
b) Gọi Ot là tia phân giác của ∠BOD
⇒ ∠O1 = ∠O2 = ∠BOD/2
Gọi Ot' là tia đối của tia Ot có OB là tia đối của tia OC
⇒ ∠O1 = ∠O4 (đối đỉnh)
Tia OD là tia đối của tia OA
⇒ ∠O2 = ∠O3 (đối đỉnh)
⇒ ∠O3 = ∠O4 = ∠BOD/2 = ∠AOC /2
⇒ Ot' là tia phân giác của ∠AOC
Mà Ot và Ot' đối nhau
⇒ Ot và Ot' cùng nằm trên 1 đường thẳng (đpcm)
Đúng 1
Bình luận (2)
Cho 2 góc kề bù AOB và AOC sao cho góc AOC =80 độ
a Tính góc AOB
b Trên cùng một nửa mặt phẳng bờ bc , chứa tia Oa vẽ tia Od sao cho BOD=140 độ . Chứng tỏ Od là tia phân giác của góc AOC
Vẽ 2 góc kề bù AOC,AOB sao cho AOC=80(độ)
a) Tính góc AOB
b)Trên cùng 1 nửa mặt phẳng bờ BC chưa tia OA vẽ tia OD sao cho góc BOD=140(độ).Chứng tỏ OD là tia phân giác của góc AOC
Xem thêm câu trả lời
Cho góc AOB = 80 độ. Gọi góc AOC và BOD là các góc kề bù với góc AOB
A. Chứng minh góc AOC và góc BOD là 2 góc đối đỉnh
B. Gọi Om, On lần lượt là các tia phân giác của góc AOC, BOD. Chứng minh Om và On là 2 tia đối nhau
Cho góc AOB = 80 độ. Gọi góc AOC và BOD là các góc kề bù với góc AOB
A. Chứng minh góc AOC và góc BOD là 2 góc đối đỉnh
B. Gọi Om, On lần lượt là các tia phân giác của góc AOC, BOD. Chứng minh Om và On là 2 tia đối nhau
(tự vẽ hình)
a) Vì góc BOD và góc AOB là hai góc đối đỉnh nên \(\widehat{BOD}=180^o-\widehat{AOB}=180^o-80^o=100^o\) (3)
=> Tia OA và tia OD đối nhau.(1)
Vì góc AOC và góc AOB là hai góc đối đỉnh nên \(\widehat{AOC}=180^o-\widehat{AOB}=180^o-80^o=100^o\) (4)
=> Tia OB và tia OC đối nhau.(2)
Từ (1);(2);(3);(4) suy ra: góc AOC và góc BOD là hai góc đối đỉnh.
b) Xét: Tia Om, On lần lượt là tia phân giác của góc AOC, BOD.
Mà góc AOC = DOB => COm= BOn
Vì CO và OB là hai tia đối nhau
=> \(\widehat{COm}+\widehat{mOB}=180^o\)
=> \(\widehat{COn}+\widehat{BOn}=180^o\)
=> \(\widehat{COm}+\widehat{BOn}=180^o\)
hay Tia Om và On là 2 tia đối nhau.
Chúc cậu học tốt!
Đúng 0
Bình luận (0)
Cho góc AOB = 80 độ, gọi góc AOC và góc BOD là các góc kề bù với góc AOB. Chứng minh
a, Hai góc AOC và BOD là hai góc đối đỉnh
b, Đường thẳng chứa tia phân giác của góc BOD cũng chứa tia phân giác của góc AOC
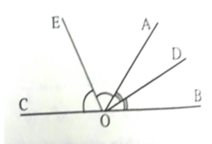
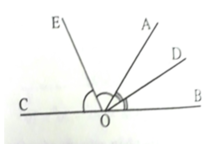
Cho 2 góc kề bù ∠AOB và ∠AOC . Hai tia OD, OE lần lượt là 2 tia phân giác của các góc ∠AOB và ∠AOC . Tính số đo góc DOE
Cho 2 góc kề bù
A
O
B
^
và
A
O
C
^
. Hai tia OD, OE lần lượt là 2 tia phân giác của các góc
A
O
B
^
và
A
O
C
^
. Tính số đo góc DOE
Đọc tiếp
Cho 2 góc kề bù A O B ^ và A O C ^ . Hai tia OD, OE lần lượt là 2 tia phân giác của các góc A O B ^ và A O C ^ . Tính số đo góc DOE
Cho 2 góc kề bù ∠AOB và ∠AOC . Hai tia OD, OE lần lượt là 2 tia phân giác của các góc ∠AOB và ∠AOC . Tính số đo góc DOE
Ủa phải có số đo của mấy góc này cụ thể chứ không có sao mà làm
Vì ^AOB và ^AOC kề bù => ^AOB + ^AOC = 1800 ( 1 )
Có ^DOE = ^AOD + ^AOE do D và E nằm khác nửa mặt phẳng bờ OA ( 2 )
^AOD = ^AOB : 2 do AD là tia phân giác ^AOB ( 3 )
^AOE = ^AOC : 2 do AE là tia phân giác ^AOE ( 4 ). Từ ( 1 )( 2 )( 3 )( 4 )
=> ^DOE = ^AOD + ^AOE = ^AOB : 2 + ^AOC : 2 = ( ^AOB + ^AOC ) : 2
= 1800 : 2 = 900. Vậy ^DOE = 900