Câu đúng: a) và g).

Câu sai: b), c), d), e), f), h).

Giải thích:

- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.

- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.

- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.

- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.

- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.

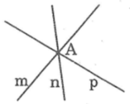
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.

△AMB nội tiếp đường tròn đường kính AB nên △AMB vuông tại M.

- Ta có: \(\widehat{CAB}+\widehat{DBA}=90^0+90^0=180^0\)

\(\Rightarrow\widehat{CAM}+\widehat{MAB}+\widehat{DBM}+\widehat{MBA}=180^0\)

\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)

\(\Rightarrow\left(\widehat{CAM}+\widehat{DBM}\right)+90^0=180^0\) nên \(\widehat{CAM}+\widehat{DBM}=90^0\)

Tứ giác ANMC có: \(\widehat{NAC}+\widehat{NMC}=90^0+90^0=180^0\)

Nên tứ giác ANMC nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CNM}\)

Tứ giác BNMD có: \(\widehat{NBD}+\widehat{NMD}=90^0+90^0=180^0\)

\(\Rightarrow\)Tứ giác BNMD nội tiếp \(\Rightarrow\widehat{MBD}=\widehat{MND}\)

\(\Rightarrow\widehat{CNM}+\widehat{MND}=\widehat{CAM}+\widehat{MBD}=90^0\)

\(\Rightarrow\widehat{INK}=90^0\).

Tứ giác MINK có: \(\widehat{IMK}+\widehat{INK}=90^0+90^0=180^0\)

\(\Rightarrow\)Tứ giác MINK nội tiếp nên \(\widehat{MIK}=\widehat{MNK}\)

Lại có \(\widehat{MNK}=\widehat{MBD}\left(cmt\right)\) \(\Rightarrow\widehat{MIK}=\widehat{MBD}\)

Xét (O): \(\widehat{MBD}=\widehat{MAB}\left(=\dfrac{1}{2}sđ\stackrel\frown{MB}\right)\)

\(\Rightarrow\widehat{MIK}=\widehat{MAB}\) nên IK//AB

Đặt s₁ ; v₁ ; t₁ lần lượt là quãng đường, vận tốc và thời gian thỏ chạy trên đồng cỏ;

      s₂ ; v₂ ; t₂ lần lượt là quãng đường, vận tốc và thời gian thỏ chạy trên đầm lầy.

Khi đó ta có tỉ số : \(v_1=\frac{s_1}{t_1};v_2=\frac{s_2}{t_2}\)

Vậy thì \(\frac{v_1}{v_2}=\frac{s_1}{t_1}:\frac{s_2}{t_2}=\frac{s_1}{t_1}.\frac{t_2}{s_2}=\frac{s_1}{s_2}.\frac{t_2}{t_1}=2.2=4\)

Vậy vận tốc của Thỏ trên đồng cỏ lớn hơn và gấp 4 lần vận tốc của Thỏ trên đầm lầy. 

vận tốc trên đồng cỏ lớn hơn và gấp 4 lần vận tốc ở đầm lầy

Vận tốc của Thỏ trên đồng cỏ lớn hơn và gấp 4 lần vận tốc của Thỏ trên đầm lầy.

a/ Ta có

^AIB=90 (góc nt chắn nửa đường tròn) => BI vuông góc AE

d vuông góc với AB tại M

=> M và I cùng nhìn BE dưới 1 góc 90 => M; I cùng nằm trên đường tròn đường kính BE => MBEI là tứ giác nội tiếp

b/ Xét tam giác vuông MEA và tam giác vuông IEH có ^AEM chung => tg MEA đồng dạng với tg IEH

d/ Xét tg ABE có

BI vuông góc AE

ME vuông góc AB

=> H là trực tâm cuat tg ABE

Ta có ^AKB =90 (góc nt chắn nửa đường tròn => AK vuông góc với BE

=> AK đi qua H (trong tam giác 3 đường cao đồng quy

=> Khi E thay đổi HK luôn đi qua A cố định

Cô hướng dẫn nhé :)

a. Ta thấy góc MBE = góc BIE = 90 độ nên từ giác MBEI nội tiếp đường tròn đường kính BE, vậy tâm là trung điểm BE.

b. \(\Delta IEH\sim\Delta MEA\left(g-g\right)\) vì có góc EIH = góc EMA = 90 độ và góc E chung.

c. Từ câu b ta có : \(\frac{IE}{EM}=\frac{EH}{EA}\Rightarrow EH.EM=IE.EA\) Vậy ta cần chứng minh \(EC.ED=IE.EA\)

Điều này suy ra được từ việc chứng minh \(\Delta IED\sim\Delta CEA\left(g-g\right)\)

Hai tam giác trên có góc E chung. góc DIE = góc ACE (Tứ giác AIDC nội tiếp nên góc ngoài bằng góc tại đỉnh đối diện) 

d. Xét tam giác ABE, ta thấy do I thuộc đường trong nên góc AIB = 90 độ. Vậy EM và BI là các đường cao, hay H là trực tâm của tam giác ABE. Ta thấy AK vuông góc BE, AH vuông góc BE, từ đó suy ra A, H ,K thẳng hàng. Vậy khi E thay đổi HK luôn đi qua A.

Tự mình trình bày để hiểu hơn nhé . Chúc em học tốt ^^