Cho tam giác ABC có AB=AC. CMR: góc B bằng góc C

Những câu hỏi liên quan
1. cho tam giác ABC có góc B = góc C. CMR AB=AC.
2. cho tam giác ABC có AB=AC. CMR góc B = góc C
minh vua tik ban do , ban tik lai minh di
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC trên cạnh AB, AC lấy D,E sao cho AD=AE CMR: Góc B = góc C và góc B bằng góc ADE
Xem chi tiết
a, Xét ΔABC có AB=AC
=> ΔABC là tam giác cân
=> Góc B = góc C (t/c)
b, Xét ΔABC có: góc A + góc B + góc C = 180 độ ( tổng 3 góc trong 1 tam giác)
=> 180 - góc A = góc B + góc C (1)
mà ΔABC là tam giác cân => góc B = góc C (2)
Xét ΔAED có AE=AD => ΔAED là tam giác cân
=> góc E = góc D (3)
Chứng minh tương tự ta có 180 độ - góc A = góc AED + góc ADE (4)
Từ (1),(2),(3),(4) => góc ADE = góc B
Đúng 0
Bình luận (0)
Bài 1: cho tam giác ABC có góc B=góc C
CMR: AB=AC
Bài 2 : Cho tam giác ABC có AB=AC; góc A= 60 độ
CMR: AB=AC=BC
Helpp mee -_-
BÀI 1 : Ta có tam giác ABC có góc B=góc C=>tam giác ABC cân tại A =>AB=AC
BÀI 2:TA có:tam giác ABC có AB=AC=>Tam giác ABC cân tại A mak koa góc A = 6O độ =>tam giác ABC đều=>AB=AC=BC
TICK NHA, MK GIẢI CHI TIẾT LẮM RÙI ĐÓ
Đúng 0
Bình luận (0)
Cho tam giác ABC góc B bằng góc C . CMR AB=AC
ta có : góc B bằng góc C (gt)
suy ra tam giác ABC là tam giác cân tại A(tính chất)
suy ra AB=AC (đpcm)
Đúng 0
Bình luận (0)
ban oi bai này cô mình chỉ cho dùng mỗi cạnh cạnh cạnh thôi
Đúng 0
Bình luận (0)
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
1. Câu hỏi của 1234567890 - Toán lớp 7 - Học toán với OnlineMath
cho tam giác ABC có AB = AC , kẻ AM vuông góc BC (M thuộc BC) a, CMR : tam giác AMB = tam giác AMC b, CMR : B = C và AM là phân giác của góc BAC c, kẻ MH , MK lần lượt vông góc với AB , AC . CMR : AH = AK
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`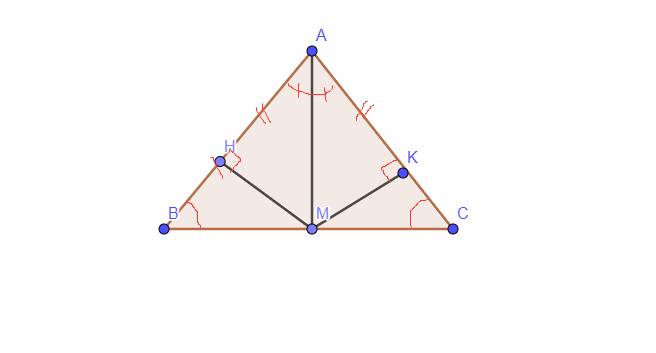
Đúng 3
Bình luận (0)
Cho tam giác ABC có góc A=90 độ và BC bằng 2 lần AB. E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D.
a) CMR: BD là tia p/g của góc ADE
b) CMR: BD=DC
c) Tính góc B và góc C của tam giác ABC
Cho tam giác ABC có AB=AC và góc B bằng góc C
Lấy điểm D trên cạnh AB, E trên cạnh AC sao cho AD=AE
Gọi I là giao điểm của BE và CD. CMR tam giác IBD bằng tam giác ICE
Cho tam giác ABC có góc B bằng góc C (góc A nhọn). Từ B hạ BH vuông góc với AC, từ C hạ CK vuông góc với AB.
1) CMR: Góc B và góc C cùng nhọn.
2) CMR: BH=CK
Cho tam giác ABC cân tại A có Ab bằng 6 com,Ac = 8 cm a, Tính Bc b,Trên tia đối của Ab lấy M sao cho AB = AM . CMR tam giác ABC bằng tam giác ACM Từ đó chứng minh CA là phân giác của góc BCM c,Kẻ Ah vuông góc BC,AK vuông góc CM. chứng minh HK song song BM d,HK cắt AC tại I. chứng minh AC là đường trung trực của HK


















