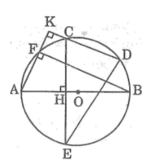
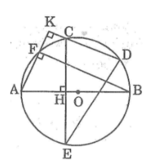
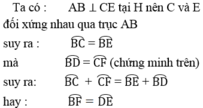Cho đường tròn (O) đường kính AB. Trên nửa đường tròn lấy 2 điểm C, D. Kẻ CH vuông góc với AB cắt đương tại điểm thứ hai là E. Ke AK vuông goác với CD cắt đường tròn tại điểm thứ 2 la F. CM: DE=BF

Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB. Trên cùng nửa đường tròn lấy hai điểm C, D. Kẻ CH vuông góc với AB tại H, CH cắt (O) tại điểm thứ hai E. Kẻ AK vuông góc với CD tại K, AK cắt (O) tại điểm thứ hai F. Chứng minh:a, Hai cung nhỏ
C
F
⏜
và
D
B
⏜
bằng nhaub, Hai cung nhỏ
B...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Trên cùng nửa đường tròn lấy hai điểm C, D. Kẻ CH vuông góc với AB tại H, CH cắt (O) tại điểm thứ hai E. Kẻ AK vuông góc với CD tại K, AK cắt (O) tại điểm thứ hai F. Chứng minh:
a, Hai cung nhỏ C F ⏜ và D B ⏜ bằng nhau
b, Hai cung nhỏ
B
F
⏜
và
D
E
⏜
bằng nhau
c, DE = BF
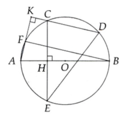
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Trên nửa đường tròn đó lấy hai điểm C, D. Kẻ CH vuông góc với AB cắt đường tròn tại điểm thứ hai E. Kẻ AK vuông góc với CD, cắt đường tròn tại điểm thứ hai F. Chứng minh rằng:
a) Hai cung nhỏ CF và DB bằng nhau.
b) DE = BF.
Thọ tested
Good!
\(e^{i\pi}=-1\)
a) Xét (O) có: AB đường kính (gt), F ϵ (O)
⇒ △ BAF vuông tại F.
⇒ BF vuông góc với AF tại F. hay BF vuông góc với KF
Mà CD vuông góc với KF tại K (gt)
⇒ CD//BF
⇒ 2 cung nhỏ CF và BD chắn 2 dây // của (O) sẽ bằng nhau.
⇒ Đcpcm
b) Ta thấy CDBF là hình thang cân ( CD//BF, CF = BD )
⇒ 2 đường chéo BC = DF. (1)
Mà △ BCE cân tại B ( vì có BH vừa là đ/c, vừa là đường trung tuyến của △)
⇒BC=BE.(2)
Từ (1) và (2) ⇒ DF = BE.
⇒ cung DF = cung BE
Cộng 2 vế trên với cung EF ta đc:
cung DE = cung BF
⇒ DE = BF
CHỨNG MINH ĐƯỢC CD//BD ( CÙNG VUÔNG GÓC AK)
=> CF=BD ( TÍNH CHẤT )
CHỨNG MINH ĐƯỢC BC=BE => CUNG BC = BE
MÀ CUNG BF= CUNG CF+ CB
CUNG DE = CUNG BD+BE
NÊN CUNG BF=CUNG DE
Xem thêm câu trả lời
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: DE = BF
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ BF và DE bằng nhau
Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng :
a) Hai cung nhỏ CF và DB bằng nhau
b) Hai cung nhỏ BF và DE bằng nhau
c) DE = BF
Cho đường tròn tâm O.Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB,nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng: Hai cung nhỏ CF và BD bằng nhau
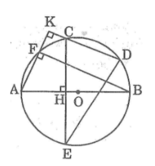
Ta có : ∆ ABF nội tiếp trong (O) và AB là đường kính cuả (O) nên ΔABF vuông tại F
Suy ra: BF ⊥ AK
Mà AK ⊥ CD (gt)
Nên : BF // CD
Suy ra: ∠ BD = ∠ CF
(hai cung bị chắn giữa hai dây song song thì bằng nhau)
Đúng 0
Bình luận (0)
Trên nửa đường tròn tâm O, đường kính AB lấy 2 điểm C và D. Kẻ CH vuông góc AB tại H, CH cắt (O) tại E. Kẻ AK vuông góc đường thẳng DC tại K, cắt (O) tại điểm thứ hai là F. Chứng minh :
a)Cung nhỏ CF = cung nhỏ DB
b)Cung nhỏ BF = cung nhỏ DE
c)DE = DF
Giúp mình vs nha !Mình cần gấp lắm !!!
Trên (O;\(\frac{AB}{2}\)) lấy 2 điểm C và D tùy ý.Kẻ CH vuông góc AB và cắt đường tròn tại điểm thứ 2 là E. Từ A kẻ AK vuông góc DC cắt đường tròn tại điểm thứ hai là F
a) CM: cung CF nhỏ = DB nhỏ.
b) CM: cung BF nhỏ = DE nhỏ
a)AKD vuông tại K
ACB vuông tại C
=> góc DCB = góc CAF ( cùng phụ với KCA)
=>cung CF =cung BD
b)cung BF = cung BC + cung CF (1)
cung DE = cung BD + cung BE
Mà BE =BC ( AB _|_CE)
cung DE = cung BD + cung BC(2)
(1)(2) =>......
Đúng 0
Bình luận (0)
C,D tùy ý là sao?
CD// AB thì không có F ?
Đúng 0
Bình luận (0)
Trên nửa đường tròn tâm O, đường kính AB lấy 2 điểm C và D. Kẻ CH vuông góc AB tại H, CH cắt (O) tại E. Kẻ AK vuông góc đường thẳng DC tại K, cắt (O) tại điểm thứ hai là F. Chứng minh :
a)Cung nhỏ CF = cung nhỏ DB
b)Cung nhỏ BF = cung nhỏ DE
c)DE = DF
giúp mình vs nha !