Tìm giá trị lớn nhất và giá trị tương ứng của x
A=|x-2|+39
Những câu hỏi liên quan
Tìm giá trị lớn nhất của biểu thức A=-x^2-y^2+xy+x+y
và các giá trị tương ứng của x và y
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
cos
x
+
1
cos
x
-
2
. Khi đó ta có: A. 9M + m 0 B. 9M - m 0 . C. M + 9m 0 D. M + m 0 .
Đọc tiếp
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có:
A. 9M + m = 0
B. 9M - m = 0 .
C. M + 9m = 0
D. M + m = 0 .
Tìm giá trị lớn nhất của các biểu thức sau và tìm giá trị tương ứng của x:
A=x2+3 B=(x-1)2 -7 C=3*(2x+1)5
Tìm giá trị nhỏ nhất và giá trị x tương ứng của M = |x - 2017| + |x - 17|
thông thường,để tổng nhỏ nhất thì có 1 số hạng = 0.
nếu lx-2017l=0=>x-2017=0=>x=2017
x-17=2000
=>M=0+2000=2000
nếu lx-17l=0=>x-17=0=>x=17
x-2017=17-2017=-2000
=>lx-2017l=l-2000l=2000
=>M=2000+0=2000
=>giá trị nhỏ nhất của M=2000 và x thuộc {17;2017}
ai ko hiểu thì ? đừng t i c k sai nha!
Đúng 0
Bình luận (0)
(15 căn x-11/x+2 căn x -3) + ( 3 căn x -2/1- căn x) - ( 2 căn x +3/ căn x +3)
a. rút gọn biểu thức
b. tìm giá trị lớn nhất của biểu thức và giá trị của x tương ứng
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x 4 – 4 x 2 + 1 trên đoạn [-1; 2]
min f(x) = f( 2 ) = −3; max f(x) = f(2) = f(0) = 1
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x – ln x + 3 trên khoảng (0; ∞ )
min f(x) = f(1) = 4. Không có giá trị lớn nhất.
Đúng 0
Bình luận (0)
Gọi M và m tương ứng giá trị lớn nhất và giá trị bé nhất của hàm số
y
x
3
+
x
2
+
x
x
2
+
1
2
.
Tính giá trị M + m ...
Đọc tiếp
Gọi M và m tương ứng giá trị lớn nhất và giá trị bé nhất của hàm số y = x 3 + x 2 + x x 2 + 1 2 . Tính giá trị M + m
A. 1
B. 2
C. 1 2
D. 3 2
Gọi M và m tương ứng giá trị lớn nhất và giá trị bé nhất của hàm số
y
x
3
+
x
2
+
x
x
2
+
1
2
.
Tính giá trị...
Đọc tiếp
Gọi M và m tương ứng giá trị lớn nhất và giá trị bé nhất của hàm số y = x 3 + x 2 + x x 2 + 1 2 . Tính giá trị M + m
A. 1
B. 2
C. 1 2
D. 3 2
Đáp án C
Có y 0 = 0.
Với x ≠ 0 ta có y = x 3 + x 2 + x x 2 x 2 + 1 2 x 2 = x + 1 x + 1 x + 1 x 2 . Đặt x + 1 x = t thì ta có y = f t = t + 1 t 2 .
Thấy v x + 1 x 2 ≥ 4. x . a x = 4 nến t 2 ≥ 4 ⇔ t ∈ − ∞ ; − 2 ∪ 2 ; + ∞ .
Có f ' t = − t 2 − 2 t t 4 . f ' t = 0 ⇔ t = 0 t = − 2
Bảng biến thiên f t với t ∈ − ∞ ; − 2 ∪ 2 ; + ∞ .
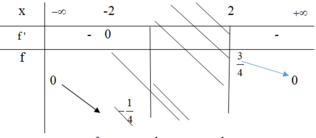
Dựa vào bảng trên thì max y = 3 4 ; min y = − 1 4 ⇒ M + m = 1 2
Đúng 0
Bình luận (0)