cho G là trọng tâm tam giac ABC và AB=c BC=a AC=b. tìm GTNN GA^2/bc+GB^2/ac+GC^2/ab

Những câu hỏi liên quan
Cho tam giác ABC có AB = AC =5cm; BC =8cm. Gọi G là trọng tâm cụa tam giác .Tính GA, GB, GC
Gọi `AM` là trung tuyến của `ΔABC`
`=>AM` đồng thời là đường cao
`=>ΔAMB;ΔAMC⊥M`
`AM` là trung tuyến nên
`BM=MC=(BC)/2=4(cm)`
Áp dụng định lý py-ta-go ta tính được
`AM^2=AB^2-BM^2=5^2-4^2=25-16=9(cm)`
`=>AM=3cm`
`G` trọng tâm
`=>GA=2/3AM=2cm`
`GM=1/3AM=1cm`
Áp dụng định lý py-ta-go lần nữa ta tính đc
`GC^2=BG^2=BM^2+GM^2=4^2+1^2=16+1=17cm`
`=>GB=GC=`\(\sqrt{17cm}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, G là trọng tâm tam giác. Vẽ đường thẳng d qua G cắt AB, AC và tia đối BC lần lượt tại C', B', A'. CMR: 1/GA'+1/GB'=1/GC'
Xem chi tiết
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC =5cm; BC =8cm. Gọi G là trọng tâm cụa tam giác .Tính GA, GB, GC
Cho tam giác ABC vuông tại A có AB a; BC 2a và G là trọng tâm. Tính giá trị của biểu thức
G
A
→
.
G
B
→
+
G
B
→
.
G
C
→
+
G
C
→
....
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
Tính giá trị của biểu thức G A → . G B → + G B → . G C → + G C → . G A
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
Chọn C.
Vì ![]() nên
nên
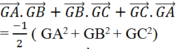
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
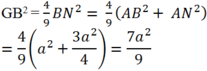
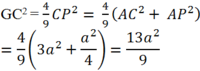
Suy ra
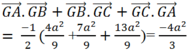
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh a, đường cao AH, trọng tâm G. Tính:
a, |AC|, |AB + AH|, |AB - AH|
b, |GB|, |GA + GB|, |GA + GB + GC|
Cho tam giác ABC có diện tích là S. BC = a, AC = b, AB = c. G là trọng tâm tam giác. Chứng minh rằng:
a/ \(cotA=\dfrac{b^2+c^2-a^2}{4S}\)
b/ \(cotA+cotB+cotC=\dfrac{a^2+b^2+c^2}{4S}\)
c/ \(GA^2+GB^2+GC^2=\dfrac{1}{3}\left(a^2+b^2+c^2\right)\)
d/ \(b^2-c^2=a\left(b.cosC-c.cosB\right)\)
a)Có \(b^2+c^2-a^2=cosA.2bc\)
\(S=\dfrac{1}{2}bc.sinA\)\(\Rightarrow4S=2bc.sinA\)
\(\Rightarrow\dfrac{b^2+c^2-a^2}{4S}=\dfrac{cosA.2bc}{2bc.sinA}=cotA\) (dpcm)
b) CM tương tự câu a \(\Rightarrow\dfrac{a^2+c^2-b^2}{4S}=\dfrac{cosB.2ac}{2ac.sinB}=cotB\); \(\dfrac{a^2+b^2-c^2}{4S}=\dfrac{cosC.2ab}{2ab.sinC}=cotC\)
Cộng vế với vế \(\Rightarrow cotA+cotB+cotC=\dfrac{b^2+c^2-a^2}{4S}+\dfrac{a^2+c^2-b^2}{4S}+\dfrac{a^2+b^2-c^2}{4S}\)\(=\dfrac{a^2+b^2+c^2}{4S}\) (dpcm)
c) Gọi ma;mb;mc là độ dài các đường trung tuyến kẻ từ đỉnh A;B;C của tam giác ABC
Có \(GA^2+GB^2+GC^2=\dfrac{4}{9}\left(m_a^2+m_b^2+m_b^2\right)\)\(=\dfrac{4}{9}\left[\dfrac{2\left(b^2+c^2\right)-a^2}{4}+\dfrac{2\left(a^2+c^2\right)-b^2}{4}+\dfrac{2\left(b^2+c^2\right)-a^2}{4}\right]\)
\(=\dfrac{4}{9}.\dfrac{3\left(a^2+b^2+c^2\right)}{4}=\dfrac{a^2+b^2+c^2}{3}\) (đpcm)
d) Có \(a\left(b.cosC-c.cosB\right)=ab.cosC-ac.cosB\)
\(=\dfrac{a^2+b^2-c^2}{2}-\dfrac{a^2+c^2-b^2}{2}\)
\(=b^2-c^2\) (dpcm)
Đúng 3
Bình luận (0)
Tam giác abc có AB =6 cm, AC =8 vm, Bc =10 cm
a) CMR: G là trongj tâm của tam giác ABC
b) tính GA+GB+GC
c) CMR: GA + GB> 2/3AB
Cho \(\Delta ABC\)có AB=AC=5cm, BC=8cm. Gọi G là trọng tâm của tam giác ABC. Tính GA;GB;GC
Bài làm:
Kẻ trung tuyến AM, CN của tam giác ABC
Vì AB = AC = 5cm => Tam giác ABC cân tại A
=> AM đồng thời là đường cao của tam giác ABC
=> AM _|_ BC
Vì M là trung điểm của BC => BM = MC = BC/2 = 4cm
Áp dụng định lý Pytago ta tính được: \(AM^2=AB^2-BM^2=5^2-4^2=9cm\)
=> AM = 3cm
=> GA = 2/3AM = 2cm ; GM = 1cm
Áp dụng Pytago lần nữa ta tính được:
\(GC^2=BG^2=BM^2+GM^2=4^2+1^2=17\)
=> \(GB=GC=\sqrt{17}cm\)
Cho tam giác ABC vuông tại A. Có AB=16cm, AC=30cm, G là trọng tâm của tam giác ABC. Tính GA+GB+GC?
1 Cho tam giác ABC, I thuộc AB, K thuộc AC kẻ IM//BK, M thuộc AC, ke KN//CI , N thuộc AB
Chứng minh MN // BC
2 Cho tam giác ABC trọng tâm G một đường thẳng qua G cắt AB tại C' cắt AC tại B' cat tia doi cua CB tai A'
a Chứng minh \(\frac{1}{GA'}+\frac{1}{GB'}=\frac{1}{GC'}\)
a. Quang tự vẽ hình nhé.
Ta thấy \(\frac{AM}{AC}=\frac{AM}{AK}.\frac{AK}{AC}\). Mà theo định lý Ta let : \(\frac{AM}{AK}=\frac{AI}{AB};\frac{AK}{AC}=\frac{AN}{AI}\)
Như vậy thì \(\frac{AM}{AC}=\frac{AI}{AB}.\frac{AN}{AI}=\frac{AN}{AB}\)
Từ đó suy ra \(\frac{AM}{AC}=\frac{AN}{AB}\) hay MN // BC.
Đúng 0
Bình luận (0)



















