XÉT BIỂU THỨC;
A= giá trị tuyệt đối của (x - \(\frac{1}{2}\))+\(\frac{3}{4}\)- x
a,Viết biểu thức A dưới dạng ko có dấu giá trị tuyệt đối
b,Tìm giá trị nhỏ nhất của A
a) Xét xem biểu thức A = 132 – 99 có chia hết cho 11 hay không?
b) Xét xem biểu thức B = 122.14 + 49. 54 – 63.12 có chia hết cho 7 hay không?
Xét biểu thức sau (3*x <=15) or (x <=4). Biểu thức cho kết quả TRUE khi:
A. x = 7
B. x = 6
C. x = 5
D. x = 8
Xét biểu thức sau (3*x <=15) and (x <=4). Biểu thức cho kết quả FALSE khi:
A. x = 3
B. x = 2
C. x = 5
D. x = 4
Xét dấu của biểu thức sau
![]()
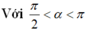
A. B > 0
B. B < 0
C. B ≥ 0
D. B ≤ 0
Xét dấu biểu thức f x = 4 x 2 - 1
f(x) = 4x2 – 1 = (2x – 1)(2x + 1)
Nhị thức 2x – 1 có nghiệm x = 1/2, nhị thức 2x + 1 có nghiệm x = –1/2.
Ta có bảng xét dấu:
Kết luận :
+ f(x) > 0 khi x < –1/2 hoặc x > 1/2.
+ f(x) < 0 khi –1/2 < x < 1/2
+ f(x) = 0 khi x = 1/2 hoặc x = –1/2.
Xét dấu biểu thức y=(x-1)^2
\(y=\left(x-1\right)^2\)
+) \(x-1=0\Leftrightarrow x=1\)
+) Vẽ trục xét dấu:
+) Ta thấy: \(y>0\) với mọi \(x\in R\); \(y< 0\) với mọi \(x\in\phi\)
Chúc bn học tốt!
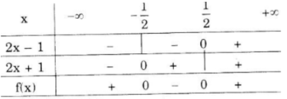
Xét dấu biểu thức: f x = - 4 3 x + 1 - 3 2 - x
Ta có:
Nhị thức –5x – 11 có nghiệm là –11/5, nhị thức 3x +1 có nghiệm là –1/3, nhị thức 2 – x có nghiệm là 2.
Ta có bảng xét dấu:
Kết luận :
+ f(x) > 0 khi –11/5 < x < –1/3 hoặc x > 2.
+ f(x) < 0 khi x < –11/5 hoặc –1/3 < x < 2.
+ f(x) = 0 khi x = –11/5.
+ Khi x = –1/3 hoặc x = 2, f(x) không xác định.
Xét dấu biểu thức sau
f(x) = x2 - x + 6
Δ=(-1)^2-4*1*6=1-24=-23<0
=>f(x) luôn cùng dấu với a=1
=>f(x)>0 với mọi x
Xét dấu biểu thức f(x) = (2x – 1)(-x + 3)

Các nghiệm này chia khoảng thành ba khoảng, trong mỗi khoảng các nhị thức đã cho có dấu hoàn toàn xác định.

Từ bảng xét dấu ta thấy:
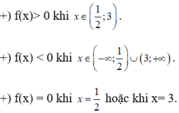
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 92: Giải bất phương trình x3 – 4x < 0.
Lời giải
x3 – 4x < 0 ⇔ x(x2 - 4) < 0 ⇔ x(x - 2)(x + 2) < 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có tập nghiệm của bất phương trình là:
S = (-∞;2) ∪ (0;2)
Nhận xét về đặc điểm của biểu thức số học